 |
Logical Conjunction and Disjunction
|
|
|
|
As mentioned already, you can nest one conditional statement
inside of another. To illustrate, imagine you create a workbook that would be used by a
real estate company that sells houses. You may face a customer who wants to
purchase a single family house but the house should not cost more than $550,001. To
implement this scenario, you can first write a procedure that asks the user
to specify a type of house and then a conditional statement would check it. Here is an example:
|
Sub Exercise
Dim TypeOfHouse As String
Dim Choice As Integer
Dim Value As Double
TypeOfHouse = "Unknown"
Choice = CInt(InputBox("Enter the type of house you want to purchase" _
& vbCrLf & _
"1. Single Family" & vbCrLf & _
"2. Townhouse" & vbCrLf & _
"3. Condominium" & vbCrLf & vbCrLf & _
"You Choice? "))
Value = CDbl(InputBox("Up to how much can you afford?"))
TypeOfHouse = Choose(Choice, "Single Family", _
"Townhouse", _
"Condominium")
End Sub
If the user selects a single family, you can then write code
inside the conditional statement of the single family. Here is an example:
Sub Exercise
Dim TypeOfHouse As String
Dim Choice As Integer
Dim Value As Double
TypeOfHouse = "Unknown"
Choice = CInt(InputBox("Enter the type of house you want to purchase" _
& vbCrLf & _
"1. Single Family" & vbCrLf & _
"2. Townhouse" & vbCrLf & _
"3. Condominium" & vbCrLf & vbCrLf & _
"You Choice? "))
Value = CDbl(InputBox("Up to how much can you afford?"))
TypeOfHouse = Choose(Choice, "Single Family", _
"Townhouse", _
"Condominium")
If Choice = 1 Then
MsgBox("Desired House Type: " & vbTab & TypeOfHouse & vbCrLf & _
"Maximum value afforded: " & vbTab & FormatCurrency(Value))
End If
End Sub
Here is an example of running the program:
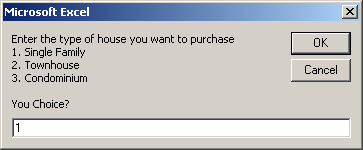
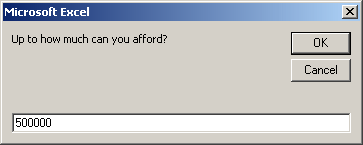
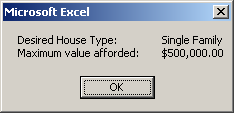
In that section, you can then write code that would request
and check the value the user entered. If that value is valid, you can take
necessary action. Here is an example:
Sub Exercise
Dim TypeOfHouse As String
Dim Choice As Integer
Dim Value As Double
TypeOfHouse = "Unknown"
Choice = CInt(InputBox("Enter the type of house you want to purchase" _
& vbCrLf & _
"1. Single Family" & vbCrLf & _
"2. Townhouse" & vbCrLf & _
"3. Condominium" & vbCrLf & vbCrLf & _
"You Choice? "))
Value = CDbl(InputBox("Up to how much can you afford?"))
TypeOfHouse = Choose(Choice, "Single Family", _
"Townhouse", _
"Condominium")
If Choice = 1 Then
MsgBox ("Desired House Type: " & vbTab & TypeOfHouse & vbCrLf & _
"Maximum value afforded: " & vbTab & FormatCurrency(Value))
If Value <= 550000 Then
MsgBox ("Desired House Matched")
Else
MsgBox ("The House Doesn't Match the Desired Criteria")
End If
End If
End Sub
|
A Conditional Conjunction |
|
Using conditional nesting, we have seen how you can write
one conditional statement that depends on another. But you must write one first condition,
check it, then nest the other condition. This works fine and there is nothing
against it.
To provide you with an alternative, you can use what is referred to
as a logical conjunction. It consists of writing one If...Then expression that
checks two conditions at the same time. To illustrate, once again consider a customer
who wants to purchase a single family home that is less than $550,000. You can consider
two statements as follows:
- The house is single family
- The house costs less than $550,000
To implement it, you would need to write an If...Then
condition as:
If The house is single family AND The house costs less than $550,000 Then
Validate
End If
In the Visual Basic language, the operator used to perform a
logical conjunction is And. Here is an example of using it:
Sub Exercise
Dim TypeOfHouse As String
Dim Choice As Integer
Dim Value As Double
TypeOfHouse = "Unknown"
Choice = _
CInt(InputBox("Enter the type of house you want to purchase" & vbCrLf & _
"1. Single Family" & vbCrLf & _
"2. Townhouse" & vbCrLf & _
"3. Condominium" & vbCrLf & vbCrLf & _
"You Choice? "))
Value = CDbl(InputBox("Up to how much can you afford?"))
TypeOfHouse = Choose(Choice, "Single Family", _
"Townhouse", _
"Condominium")
If TypeOfHouse = "Single Family" And Value <= 550000 Then
MsgBox("Desired House Type: " & vbTab & TypeOfHouse & vbCrLf & _
"Maximum value afforded: " & vbTab & FormatCurrency(Value))
MsgBox("Desired House Matched")
Else
MsgBox("The House Doesn't Match the Desired Criteria")
End If
End Sub
Here is an example of running the program:

By definition, a logical conjunction combines two
conditions. To make the program easier to read, each side of the conditions can
be included in parentheses. Here is an example:
Sub Exercise
. . . No Change
If (TypeOfHouse = "Single Family") And (Value <= 550000) Then
MsgBox("Desired House Type: " & vbTab & TypeOfHouse & vbCrLf & _
"Maximum value afforded: " & vbTab & FormatCurrency(Value))
MsgBox("Desired House Matched")
Else
MsgBox("The House Doesn't Match the Desired Criteria")
End If
End Sub
To understand how logical conjunction works, from a list of real estate properties,
after selecting the house type, if you find a house
that is a single family home, you put it in the list of considered properties:
| Type of House |
House |
| The house is single family |
True |

If you find a house that is less than or
equal to $550,000, you retain it:
| Price Range |
Value |
| $550,000 |
True |
For the current customer, you want a house to meet BOTH criteria. If the
house is a town house, based on the request of our customer, its conditional
value is false. If the house is less than $550,000, such as $485,000, the value of the Boolean
Value is true:

If the
house is a town house, based on the request of our customer, its conditional
value is false. If the house is more than $550,000, the value of the Boolean
Value is true. In logical conjunction, if one of the conditions is false, the
result if false also.
This can be illustrated as follows:
| Type of House |
House Value |
Result |
| Town House |
$625,000 |
Town House AND $625,000 |
| False |
False |
False |
Suppose we find a single family home. The first condition is
true for our customer. With the AND Boolean operator, if the first condition is
true, then we consider the second criterion. Suppose that the house we are
considering costs $750,500: the price is out of the customer's range. Therefore,
the second condition is false. In the AND Boolean algebra, if the second
condition is false, even if the first is true, the whole condition is false.
This would produce the following table:
| Type of House |
House Value |
Result |
| Single Family |
$750,500 |
Single Family AND $750,500 |
| True |
False |
False |
Suppose we find a townhouse that costs $420,000. Although
the second condition is true, the first is false. In Boolean algebra, an AND
operation is false if either condition is false:
| Type of House |
House Value |
Result |
| Town House |
$420,000 |
Town House AND $420,000 |
| False |
True |
False |
If we find a single family home that costs $345,000, both
conditions are true. In Boolean algebra, an AND operation is true if BOTH
conditions are true. This can be illustrated as follows:
| Type of House |
House Value |
Result |
| Single Family |
$345,000 |
Single Family AND $345,000 |
| True |
True |
True |
These four tables can be resumed as follows:
| If Condition1 is |
If Condition2 is |
Condition1
AND
Condition2 |
| False |
False |
False |
| False |
True |
False |
| True |
False |
False |
| True |
True |
True |
As you can see, a logical conjunction is true only of BOTH
conditions are true.
As seen above, the logical conjunction operator is used to
combine two conditions. In some cases, you will need to combine more than two
conditions. Imagine a customer wants to purchase a single family house that
costs up to $450,000 with an indoor garage. This means that the house must
fulfill these three requirements:
- The house is a single family home
- The house costs less than $450,001
- The house has an indoor garage
Here is the program that could be used to check these
conditions:
Sub Exercise
Dim TypeOfHouse As String
Dim Choice As Integer
Dim Value As Double
Dim IndoorGarageAnswer As Integer
Dim Answer As String
TypeOfHouse = "Unknown"
Choice = _
CInt(InputBox("Enter the type of house you want to purchase" _
& vbCrLf & _
"1. Single Family" & vbCrLf & _
"2. Townhouse" & vbCrLf & _
"3. Condominium" & vbCrLf & vbCrLf & _
"You Choice? "))
Value = CDbl(InputBox("Up to how much can you afford?"))
TypeOfHouse = Choose(Choice, "Single Family", _
"Townhouse", _
"Condominium")
IndoorGarageAnswer = _
MsgBox("Does the house have an indoor garage (1=Yes/0=No)?", _
vbQuestion Or vbYesNo, _
"Real Estate")
Answer = IIf(IndoorGarageAnswer = vbYes, "Yes", "No")
If (TypeOfHouse = "Single Family") And _
(Value <= 550000) And _
(IndoorGarageAnswer = vbYes) Then
MsgBox "Desired House Type: " & vbTab & TypeOfHouse & vbCrLf & _
"Maximum value afforded: " & vbTab & _
FormatCurrency(Value) & vbCrLf & _
"House has indoor garage: " & vbTab & Answer
MsgBox "Desired House Matched"
Else
MsgBox ("The House Doesn't Match the Desired Criteria")
End If
End Sub
We saw that when two conditions are combined, the interpreter
first checks the first condition, followed by the second. In the same way, if
three conditions need to be considered, the interpreter evaluates the truthfulness
of the first condition:
| Type of House |
| A |
| Town House |
| False |
If the first condition (or any condition) is false, the
whole condition is false, regardless of the outcome of the other(s). If the
first condition is true, then the second condition is evaluated for its
truthfulness:
| Type of House |
Property Value |
| A |
B |
| Single Family |
$655,000 |
| True |
False |
If the second condition is false, the whole combination is
considered false:
| A |
B |
A AND B |
| True |
False |
False |
When evaluating three conditions, if either the first or the
second is false, since the whole condition would become false, there is no
reason to evaluate the third. If both the first and the second conditions are
false, there is also no reason to evaluate the third condition. Only if the
first two conditions are true will the third condition be evaluated whether it
is true:
| Type of House |
Property Value |
Indoor Garage |
| A |
B |
C |
| Single Family |
$425,650 |
None |
| True |
True |
False |
The combination of these conditions in a logical conjunction
can be written as A AND B AND C. If the third condition is false, the whole
combination is considered false:
| A |
B |
A AND B |
C |
A AND B AND C |
| True |
True |
True |
False |
False |
From our discussion so far, the truth table of the
combinations can be illustrated as follows:
| A |
B |
C |
A AND B AND C |
| False |
Don't Care |
Don't Care |
False |
| True |
False |
Don't Care |
False |
| True |
True |
False |
False |
The whole combination is true only if all three conditions
are true. This can be illustrated as follows:
| A |
B |
C |
A AND B AND C |
| False |
False |
False |
False |
| False |
False |
True |
False |
| True |
False |
False |
False |
| True |
False |
True |
False |
| False |
True |
False |
False |
| False |
True |
True |
False |
| True |
True |
False |
False |
| True |
True |
True |
True |