Home

Microsoft Visual C# Application: Probability Distribution
     

Introduction

In statistics, a random variable is a numerical value gotten by chance. For example, if you have a coin and throw it up. When it falls, either of the sides, the face or the back, should have the same likelihood of being selected, that is, of facing up. The face that shows up has a value referred to as a random variable. The likelihood of something occuring is called a probability.

A random variable is usually expressed as x.

A probability distribution is the probability that a random variable would occur.

In most calculations, both the random variables and the probabilities (of each random variable occuring) are given to you, as a list or in a table.

The sum of all probabilities is expressed as:

ΣP(x)

To have an effective probability distribution, the values considered must follow these two requirements:
  1. Σ(x) = 1: The sum of all probabilities must be equal to 1
  2. 0 ≤ P(x) ≤ 1: Each value of the probabilities must be between 0 and 1 included

If these two requirements are met, then you can perform your calculations.

ApplicationApplication: Starting the Application
  1. Start Microsoft Visual Studio
  2. To create a new application, on the main menu, click File -> New Project...
  3. In the middle list, click Windows Forms Application
  4. Change the Name to ProbabilityDistribution1
  5. Click OK
  6. In the Solution Explorer, right-click Form1.cs and click Rename
  7. Type Exercise.cs and press Enter
  8. Design the form as follows:
     
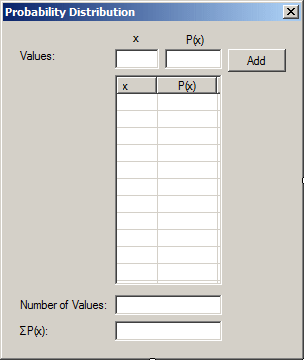    Probability Distribution
    Control Name Text
    Label Label   Values:
    Label Label   x
    Label Label   P(x)
    TextBox ListBox txtX  
    TextBox ListBox txtPofX  
    Button Button btnAdd Add
    ListView Label lvwValues FullRowSelect: True
    GridLines: True
    View: Details
    Columns  
    (Name) Text TextAlign Width
    colX x   40
    colPofX P(x) Center  
    Label Label   Number of Values:
    TextBox Text Box txtCount  
    Label Label   ΣP(x):
    TextBox Text Box txtSum  
  9. Double-click an unoccupied area of the form
  10. Change the file as follows: 
    using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;

namespace ProbabilityDistribution1
{
    public partial class Exercise : Form
    {
        List<Distribution> values;

        public Exercise()
        {
            InitializeComponent();
        }

        private void Exercise_Load(object sender, EventArgs e)
        {
            values = new List<Distribution>();
        }

        void ShowValues()
        {
            double sum = 0.00;
            lvwValues.Items.Clear();

            foreach(Distribution dist in values)
            {
                ListViewItem lviValue = new ListViewItem(dist.X.ToString());
                lviValue.SubItems.Add(dist.PofX.ToString());
                lvwValues.Items.Add(lviValue);
            }

            txtCount.Text = values.Count.ToString();

	    // Calculate the sum of the P(x) values
	    foreach (Distribution d in values)
        	sum += d.PofX;
	    txtSum.Text = sum.ToString();
        }
    }

    public class Distribution
    {
        public int X { get; set; }
        public double PofX { get; set; }

        public Distribution(int x, double p)
        {
            X = x;
            PofX = p;
        }
    }
}
  11. Return to the form and double-click the Add button
  12. Implement the event as follows: 
    private void btnAdd_Click(object sender, EventArgs e)
{
    int x = 0;
    double p = 0.00, sum = 0.00;
    Distribution dist = null;

    // Check that the user entered a value for x
    if (txtX.Text.Length == 0)
    {
        MessageBox.Show("You must enter the x value.",
                        "Probability Distribution");
        return;
    }

    // Test that the user entered a value for P(x)
    if (txtPofX.Text.Length == 0)
    {
        MessageBox.Show("You must enter the P(x) value.",
                        "Probability Distribution");
        return;
    }

    // Get the value for x
    try
    {
        x = int.Parse(txtX.Text);
    }
    catch (FormatException)
    {
        MessageBox.Show("The value you entered is invalid.",
                        "Probability Distribution");
    }

    // Get the value for P(x)
    try
    {
        p = double.Parse(txtPofX.Text);
    }
    catch (FormatException)
    {
        MessageBox.Show("The value you entered is invalid.",
                        "Probability Distribution");
    }

    // Create a Distribution value
    dist = new Distribution(x, p);
    // Add the value to the list
    values.Add(dist);

    ShowValues();

    // Calculate the sum of the P(x) values
    foreach (Distribution d in values)
        sum += d.PofX;
    txtSum.Text = sum.ToString("F");

    txtX.Text = "";
    txtPofX.Text = "";
    txtX.Focus();

    // Test the first requirement
    if (sum != 1) // The first rule is not respected
    {
        MessageBox.Show("The first rule is not respected",
                        "Probability Distribution");
        return;
    }

    // Test the second requirement
    foreach (Distribution d in values)
    {
        if ((d.PofX < 0.00) || (d.PofX > 1)) // The second rule is not respected
        {
            MessageBox.Show("The second rule is not respected",
                            "Probability Distribution");
            return;
        }
    }
}
  13. Return to the form
  14. To execute, press F5
  15. Enter values and click Add each time
     
    Random Variables
  16. Close the form and return to your programming environment

The Mean of a Probability Distribution

The mean is the average of a set. To calculate it for a probability distribution, use the following formula:

µ = Σ[x . P(x)]

ApplicationApplication: Calculating the Mean of Probability Distribution
  1. Change the design of the form as follows:
     
    Probability Distribution
    Control Name Text
    ListView Label lvwValues FullRowSelect: True
    GridLines: True
    View: Details
    Columns  
    (Name) Text TextAlign Width
    colX x   40
    colPofX P(x) Center  
    colXTimesPofX x . P(x) Center 100
    Label Label   Mean of Probability Distribution:
    TextBox Text Box txtMean  
  2. Double-click the Add button
  3. change the event as follows: 
     void ShowValues()
{
    double sum = 0.00;
    double mean = 0.00;
    lvwValues.Items.Clear();

    foreach (Distribution dist in values)
    {
        ListViewItem lviValue = new ListViewItem(dist.X.ToString());
        lviValue.SubItems.Add(dist.PofX.ToString());
        mean += dist.X * dist.PofX;
        lviValue.SubItems.Add(dist.X.ToString() + " * " +
                              dist.PofX.ToString() + " = " +
                              mean.ToString());
        lvwValues.Items.Add(lviValue);
    }

    foreach (Distribution d in values)
        sum += d.PofX;

    txtCount.Text = values.Count.ToString();
    txtSum.Text = sum.ToString();
    txtMean.Text = mean.ToString();
}
  4. To execute, press F5
  5. Type some values and click Add after each
     
    Probability Distribution
  6. Close the form and return to your programming environment

The Variance for a Probability Distribution

A variance is a process of representing a probability distribution by showing by how much the values of a series are away of the mean.

The formula to calculate the variance for a probability distribution is:

σ2 = Σ[(x - µ)2 . P(x)]

Another formula you can use is:

σ2 = Σ[x2 . P(x)] - µ2

ApplicationApplication: Calculating the Variance
  1. Change the design of the form as follows:
     
    Random Variables
    Control (Name) Text
    ListView Label lvwValues FullRowSelect: True
    GridLines: True
    View: Details
    Columns  
    (Name) Text TextAlign Width
    colX x   40
    colPofX P(x) Center  
    colXTimesPofX x . P(x) Center 100
    colVariance (x - µ)2 * P(x)   180
    Label Label   Variance of Probability Distribution:
    TextBox Text Box txtVariance  
  2. Double-click the Calculate button
  3. Change the file as follows: 
    . . . No Change

void ShowValues()
{
    lvwValues.Items.Clear();

    foreach (Distribution dist in values)
    {
        ListViewItem lviValue = new ListViewItem(dist.X.ToString());
        lviValue.SubItems.Add(dist.PofX.ToString());

        lviValue.SubItems.Add(dist.X.ToString() + " * " +
                              dist.PofX.ToString() + " = " +
                              (dist.X * dist.PofX).ToString());
        lvwValues.Items.Add(lviValue);
    }

    txtCount.Text = values.Count.ToString();
}

. . . No Change

private void btnCalculate_Click(object sender, EventArgs e)
{
    double mean = 0.00, variance = 0.00;

    foreach (Distribution dist in values)
        mean += (dist.X * dist.PofX);

    lvwValues.Items.Clear();

    foreach (Distribution dist in values)
    {
        ListViewItem lviValue = new ListViewItem(dist.X.ToString());
        lviValue.SubItems.Add(dist.PofX.ToString());

        lviValue.SubItems.Add(dist.X.ToString() + " * " + 
                              dist.PofX.ToString() + " = " +
                              (dist.X * dist.PofX).ToString());
        lviValue.SubItems.Add("(" + dist.X.ToString() + " - " +
                              mean.ToString() + ")² * " +
                              dist.PofX.ToString() + " = " +
                              Math.Pow(dist.X - mean, 2) * dist.PofX);
        lvwValues.Items.Add(lviValue);
    }

    foreach (Distribution dist in values)
        variance += Math.Pow(dist.X - mean, 2) * dist.PofX;

    txtMean.Text = mean.ToString();
    txtVariance.Text = variance.ToString();
}
  4. Return to the form
  5. To execute, press F5
  6. Test the form with some values:
     
    Random Variables
  7. Click Calculate
     
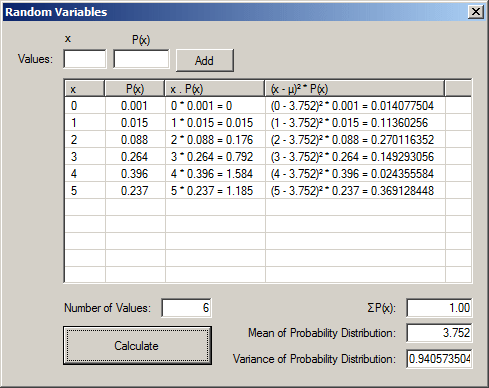
    Random Variables
  8. Close the form and return to your programming environment

The Standard Deviation for a Probability Distribution

The standard deviation is a value that indicates by how much the elements of a series vary from the mean. The formula to calculate the standard deviation for a probability distribution is:

Standard Deviation

ApplicationApplication: Calculating the Standard Deviation
  1. Change the design of the form as follows:
     
    Standard Deviation for Probability Distribution
    Control (Name) Text
    ListView Label lvwValues FullRowSelect: True
    GridLines: True
    View: Details
    Label Label   Standard Deviation of Probability Distribution:
    TextBox Text Box txtStdDev  
    Button Button btnClear Clear
    Button Button btnClose Close
  2. Double-click the Calculate button
  3. Return to the form
  4. Double-click the Clear button
  5. Return to the form
  6. Double-click the Close button
  7. Change the file as follows: 
    using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;

namespace ProbabilityDistribution1
{
    public partial class Exercise : Form
    {
        List<Distribution> values;

        public Exercise()
        {
            InitializeComponent();
        }

        private void Exercise_Load(object sender, EventArgs e)
        {
            values = new List<Distribution>();
        }

        void ShowValues()
        {
            lvwValues.Items.Clear();

            foreach (Distribution dist in values)
            {
                ListViewItem lviValue = new ListViewItem(dist.X.ToString());
                lviValue.SubItems.Add(dist.PofX.ToString());

                lviValue.SubItems.Add(dist.X.ToString() + " * " +
                                      dist.PofX.ToString() + " = " +
                                      (dist.X * dist.PofX).ToString());
                lvwValues.Items.Add(lviValue);
            }

            txtCount.Text = values.Count.ToString();
        }

        private void btnAdd_Click_1(object sender, EventArgs e)
        {
            int x = 0;
            double p = 0.00, sum = 0.00;
            Distribution dist = null;

            // Check that the user entered a value for x
            if (txtX.Text.Length == 0)
            {
                MessageBox.Show("You must enter the x value.",
                                "Probability Distribution");
                return;
            }

            // Test that the user entered a value for P(x)
            if (txtPofX.Text.Length == 0)
            {
                MessageBox.Show("You must enter the P(x) value.",
                                "Probability Distribution");
                return;
            }

            // Get the value for x
            try
            {
                x = int.Parse(txtX.Text);
            }
            catch (FormatException)
            {
                MessageBox.Show("The value you entered is invalid.",
                                "Probability Distribution");
            }

            // Get the value for P(x)
            try
            {
                p = double.Parse(txtPofX.Text);
            }
            catch (FormatException)
            {
                MessageBox.Show("The value you entered is invalid.",
                                "Probability Distribution");
            }

            // Create a Distribution value
            dist = new Distribution(x, p);
            // Add the value to the list
            values.Add(dist);

            ShowValues();

            // Calculate the sum of the P(x) values
            foreach (Distribution d in values)
                sum += d.PofX;
            txtSum.Text = sum.ToString("F");

            txtX.Text = "";
            txtPofX.Text = "";
            txtX.Focus();

            // Test the requirements of probability distribution
            if (sum != 1) // The first rule is not respected
            {
                MessageBox.Show("The first rule is not respected",
                                "Probability Distribution");
                return;
            }

            foreach (Distribution d in values)
            {
            	// Check the second requirement
                if ((d.PofX < 0.00) || (d.PofX > 1))
                {
                    MessageBox.Show("The second rule is not respected",
                                    "Probability Distribution");
                    return;
                }
            }
        }

        private void btnCalculate_Click(object sender, EventArgs e)
        {
            double mean = 0.00, variance = 0.00;
            double sum = 0.00, stddev = 0.00;

            foreach (Distribution dist in values)
                mean += (dist.X * dist.PofX);

            lvwValues.Items.Clear();

            foreach (Distribution dist in values)
            {
                ListViewItem lviValue = new ListViewItem(dist.X.ToString());
                lviValue.SubItems.Add(dist.PofX.ToString());

                lviValue.SubItems.Add(dist.X.ToString() + " * " +
                                      dist.PofX.ToString() + " = " +
                                      (dist.X * dist.PofX).ToString());
                lviValue.SubItems.Add("(" + dist.X.ToString() + " - " +
                                      mean.ToString() + ")2 * " +
                                      dist.PofX.ToString() + " = " +
                                      Math.Pow(dist.X - mean, 2) * dist.PofX);
                lvwValues.Items.Add(lviValue);
            }

            foreach (Distribution dist in values)
                variance += Math.Pow(dist.X - mean, 2) * dist.PofX;

            foreach (Distribution dist in values)
                sum += Math.Pow(dist.X, 2) * dist.PofX;

            stddev = Math.Sqrt(sum - Math.Pow(mean, 2));

            txtMean.Text = mean.ToString();
            txtVariance.Text = variance.ToString();
            txtStdDev.Text = stddev.ToString();
        }

        private void btnClear_Click(object sender, EventArgs e)
        {
            txtX.Text = "";
            txtPofX.Text = "";
            lvwValues.Items.Clear();
            txtCount.Text = "";
            txtSum.Text = "";
            txtMean.Text = "";
            txtVariance.Text = "";
            txtStdDev.Text = "";
        }

        private void btnClose_Click(object sender, EventArgs e)
        {
            Close();
        }
    }

    public class Distribution
    {
        public int X { get; set; }
        public double PofX { get; set; }

        public Distribution(int x, double p)
        {
            X = x;
            PofX = p;
        }
    }
}
  8. To execute, press F5
  9. Test the form with some values:
     
    Standard Deviation for Probability Distribution
  10. Click Calculate
     
    Standard Deviation for Probability Distribution
  11. Close the form and return to your programming environment

Application

 
Home Copyright © 2010-2016, FunctionX