Trigonometric Functions
Trigonometric Functions
Trigonometry
Introduction
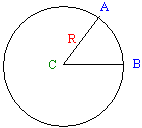
A circle is a group or series of distinct points drawn at an exact same distance from another point referred to as the center. The distance from the center C to one of these equidistant points is called the radius, R. The line that connects all of the points that are equidistant to the center is called the circumference of the circle. The diameter is the distance between two points of the circumference to the center; in other words, a diameter is double the radius.
To manage the measurements and other related operations, the circumference is divided into 360 portions. Each of these portions is called a degree. The unit used to represent the degree is the degree, written as ˚. Therefore, a circle contains 360 degrees, that is 360˚. The measurement of two points A and D of the circumference could have 15 portions of the circumference. In this case, this measurement would be represents as 15˚.
The distance between two equidistant points A and B is a round shape geometrically defined as an arc. An angle is the ratio of the distance between two points A and B of the circumference divided by the radius R. This can be written as:
Therefore, an angle is the ratio of an arc over the radius. Because an angle is a ratio and not a "physical" measurement, which means an angle is not a dimension, it is independent of the size of a circle. Obviously this angle represents the number of portions included by the three points. A better unit used to measure an angle is the radian or rad.
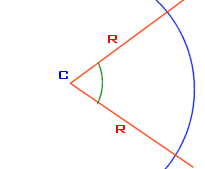
A cycle is a measurement of the rotation around the circle. Since the rotation is not necessarily complete, depending on the scenario, a measure is made based on the angle that was covered during the rotation. A cycle could cover part of the circle in which case the rotation would not have been completed. A cycle could also cover the whole 360˚ of the circle and continue there after. A cycle is equivalent to the radian divided by 2 * Pi.
![]() Practical Learning: Introducing Trigonometry
Practical Learning: Introducing Trigonometry
|
|
|
|
body {
}
.bold { font-weight: bold; }
.text-right { text-align: right }
.delimiter { margin: auto;
width: 650px; }
.top-bar { border-bottom: 6px solid blue;
background-color: #800000 !important; }
.common-font { font-family: Georgia, Garamond, 'Times New Roman', serif; }
.navbar-light .navbar-brand { color: white; }
.navbar-light .navbar-brand:hover { color: yellow; }
.navbar-light .navbar-brand:focus { color: khaki; }
.navbar-light .navbar-brand { font-family: Georgia, Garamond, 'Times New Roman', serif; }
.nav-link { font-family: Georgia, Garamond, 'Times New Roman', serif; }<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="utf-8" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>@ViewData["Title"] - Oblique Triangles</title>
<link rel="stylesheet" href="~/lib/bootstrap/dist/css/bootstrap.min.css" />
<link rel="stylesheet" href="~/css/site.css" asp-append-version="true" />
<link rel="stylesheet" href="~/css/Geometry.css" asp-append-version="true" />
</head>
<body>
<header>
<nav class="navbar navbar-expand-sm navbar-toggleable-sm navbar-light bg-white border-bottom box-shadow mb-3 top-bar">
<div class="container">
<a class="navbar-brand" asp-area="" asp-page="/Index">Oblique Triangles</a>
<button class="navbar-toggler" type="button" data-bs-toggle="collapse" data-bs-target=".navbar-collapse" aria-controls="navbarSupportedContent"
aria-expanded="false" aria-label="Toggle navigation">
<span class="navbar-toggler-icon"></span>
</button>
<div class="navbar-collapse collapse d-sm-inline-flex justify-content-between">
<ul class="navbar-nav flex-grow-1">
<li class="nav-item">
<a class="nav-link text-white" asp-area="" asp-page="/AAS">AAS</a>
</li>
<li class="nav-item">
<a class="nav-link text-white" asp-area="" asp-page="/SAS">SAS</a>
</li>
<li class="nav-item">
<a class="nav-link text-white" asp-area="" asp-page="/ASA">ASA</a>
</li>
<li class="nav-item">
<a class="nav-link text-white" asp-area="" asp-page="/SSS">SSS</a>
</li>
</ul>
</div>
</div>
</nav>
</header>
<div class="container">
<main role="main" class="pb-3">
@RenderBody()
</main>
</div>
<footer class="border-top footer text-muted">
<div class="container">
<p class="text-center common-font">© 2022 - Oblique Triangles - <a asp-area="" asp-page="/Privacy">Privacy</a></p>
</div>
</footer>
<script src="~/lib/jquery/dist/jquery.min.js"></script>
<script src="~/lib/bootstrap/dist/js/bootstrap.bundle.min.js"></script>
<script src="~/js/site.js" asp-append-version="true"></script>
@await RenderSectionAsync("Scripts", required: false)
</body>
</html>The PI Constant
The letter п, also written as Pi, is a constant number used in various mathematical calculations. Its approximate value is 3.1415926535897932. The calculator of Microsoft Windows represents it as 3.1415926535897932384626433832795.
To support the Pi constant, the Math class is equipped with a constant named PI.
A diameter is two times the radius. In geometry, it is written as 2R. In C++, it is written as 2 * R or R * 2 (because the multiplication is symmetric). The circumference of a circle is calculated by multiplying the diameter to Pi, which is 2Rп, or 2 * R * п or 2 * R * Pi.
A radian is 2Rп/R radians or 2Rп/R rad, which is the same as 2п rad or 2 * Pi.
To perform conversions between the degree and the radian, you can use the formula:
360˚ = 2п rad which is equivalent to 1 rad = 360˚ / 2п = 57.3˚.
The Sine of a Value
Consider a right triangle as follows:
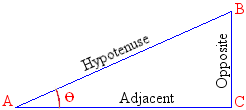
Consider AB the length of A to B, also called the hypotenuse to point A. Also consider CB the length of C to B, which is the opposite side to point A. The sine of an angle represents the ratio of CB/AB; that is, the ratio of the opposite side, CB, over the hypotenuse AB.
In trigonometry, the sine is written as sin. If x is the angle on which you are working. Its sine value would be written as sin(x) (expressed as the sine of x). If the value you want to find is named y, it means you are trying to solve the equation:
y = sin(x)
To let you calculate the sine of a value, the Math class proposes a function named Sin(). Its syntax is:
public static double Sin(double a);
When calling this function, pass the value of the angle. The function would then produce the sine value. Here is an example:
@page
@model Valuable.Pages.CreatureModel
@{
double number = 82.55;
double sine = Math.Asin(number);
}
<pre>========================================
The sine of @number is @sine
========================================</pre>
This would produce:
======================================== The sine of 82.55 is 0.7634196223225193 ========================================
![]() Practical Learning: Introducing the Sine Value
Practical Learning: Introducing the Sine Value
@page
@model ObliqueTriangles1.Pages.AASModel
@{
string? strMessage = null;
double side1 = 0.00, side2 = 0.00, side3 = 0.00;
double angle1 = 0.00, angle2 = 0.00, angle3 = 0.00;
if (Request.HasFormContentType)
{
try
{
angle1 = double.Parse(Request.Form["txtAASAngle1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the lower left angle of the AAS shape.";
}
try
{
angle2 = double.Parse(Request.Form["txtAASAngle2"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the lower right angle of the AAS shape.";
}
try
{
side1 = double.Parse(Request.Form["txtAASSide1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the right side of the AAS shape.";
}
// Here, we use the law of sines
angle3 = 180 - (angle1 + angle2);
side2 = side1 * Math.Sin(angle2 * Math.PI / 180) / Math.Sin(angle1 * Math.PI / 180);
side3 = side1 * Math.Sin(angle3 * Math.PI / 180) / Math.Sin(angle1 * Math.PI / 180);
}
}
<div class="delimiter common-font">
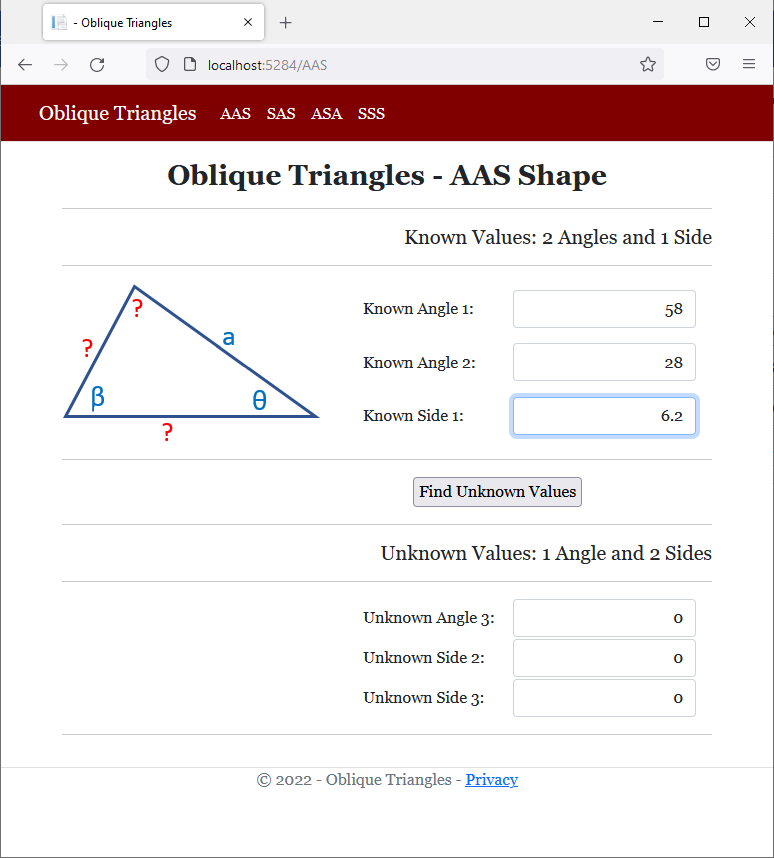
<h2 class="text-center bold">Oblique Triangles - AAS Shape</h2>
<hr />
<h5 class="text-right">Known Values: 2 Angles and 1 Side</h5>
<hr />
<form name="frmGeometry" method="post">
<table>
<tr>
<td style="width: 300px" rowspan="3">
<img src="~/images/aas.png" width="258" height="159" alt="Oblique Triangles - AAS Shape">
</td>
<td style="width: 150px">Known Angle 1:</td>
<td>@Html.TextBox("txtAASAngle1", @angle1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Angle 2:</td>
<td>@Html.TextBox("txtAASAngle2", @angle2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 1:</td>
<td>@Html.TextBox("txtAASSide1", @side1, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<table>
<tr>
<td style="width: 350px"> </td>
<td style="text-align: center"><input type="submit" name="btnSubmit" value="Find Unknown Values" /></td>
</tr>
</table>
</form>
<hr />
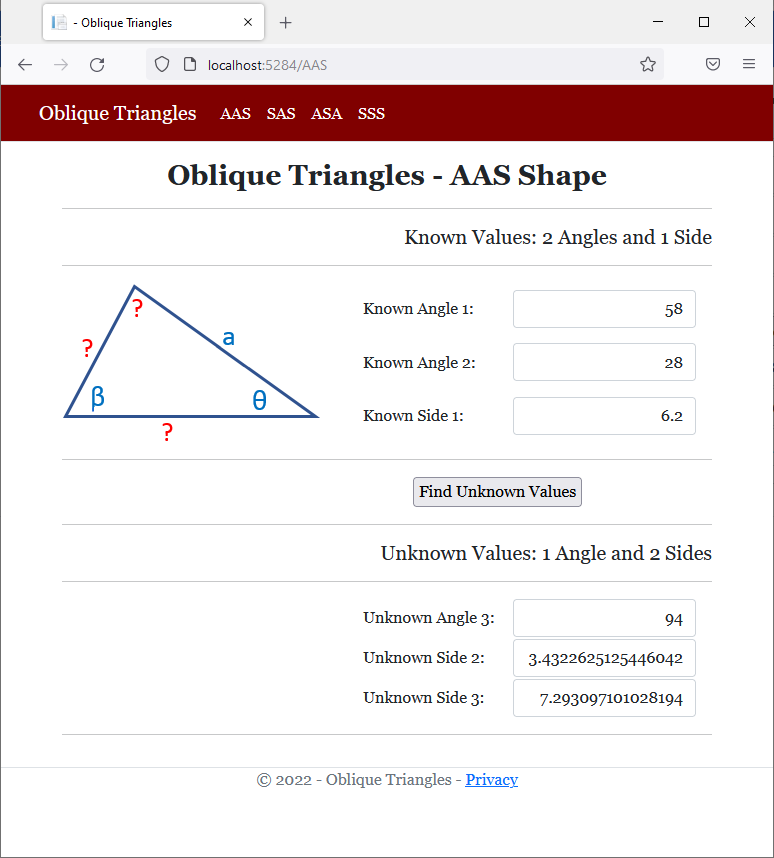
<h5 class="text-right">Unknown Values: 1 Angle and 2 Sides</h5>
<hr />
<table>
<tr>
<td style="width: 300px"> </td>
<td style="width: 150px">Unknown Angle 3:</td>
<td>@Html.TextBox("txtAASAngle3", @angle3, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Side 2:</td>
<td>@Html.TextBox("txtAASSide2", @side2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Side 3:</td>
<td>@Html.TextBox("txtAASSide3", @side3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<p class="text-center">@strMessage</p>
</div>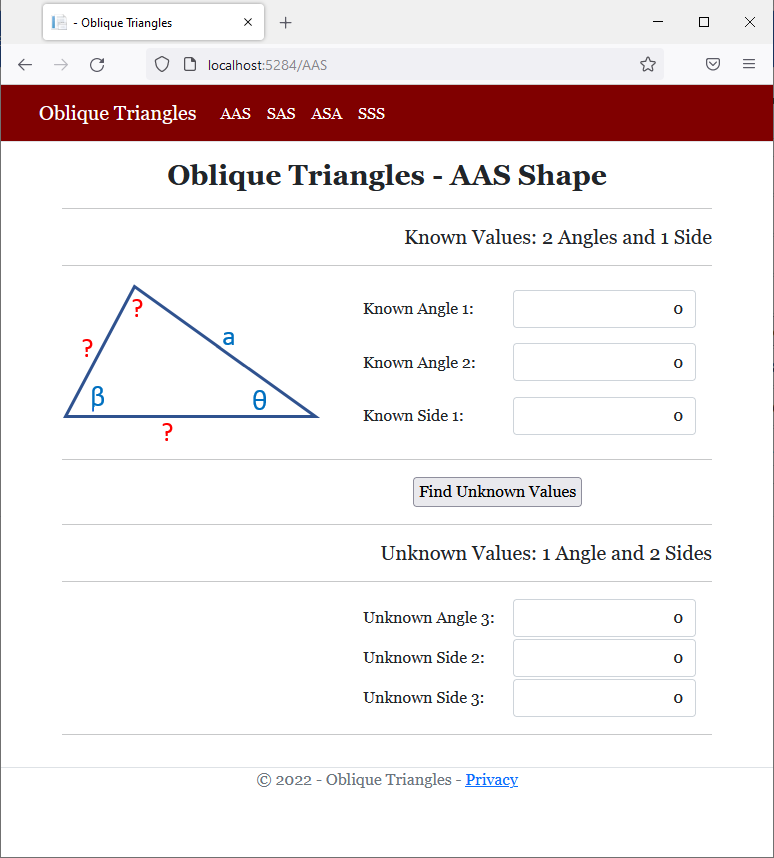
The Arc Sine of a Number
Now that we have seen how to define the sine of an angle of a right triangle, we can define the opposite of a sine as the arc sine of an angle. In a trigonometric course, the arc sine is written as arcsin. We saw that, if x is an angle, its sine is y = sin(x). In this case, the arc sine is:
x = arcsin(y)
The value of y must be between -1 (included) and 1 (included). To let you calculate the arc sine of an angle, the Math class is equipped with a function named Asin. Its takes one argument. The syntax of this function is:
public static double Asin (double d);
Pass the value of the angle to this function. Here is an example:
@page
@model Valuable.Pages.CreatureModel
@{
double number = .746;
double sine = Math.Sin(number);
double arcsine = Math.Asin(number);
}
<pre>==============================================
The sine of @number is @sine
The arc sine of @number is @arcsine
==============================================</pre>}
This would produce:
============================================== The sine of 0.746 is 0.6787065592497046 The arc sine of 0.746 is 0.842035204195032 ==============================================
The Cosine of a Value
Once again, consider the following right triangle:

Consider AB the length of A to B, also referred to as the hypotenuse. Also consider AC the length of A to C which is the side adjacent to point A. The cosine of the angle at point A is the ratio AC/AB. That is, the ratio of the adjacent length, AC, over the length of the hypotenuse, AB:
The returned value, the ratio, is a double-precision number between -1 and 1.
To calculate the cosine of an angle, the Math class provides the Cos() method. Its syntax is:
public static double Cos(double d);
Here is an example:
@page
@model Valuable.Pages.CreatureModel
@{
int number = 82;
double nbr = Math.Cos(number);
}
<pre>=======================================
The cosine of @number is @nbr
=======================================</pre>
This would produce:
======================================= The cosine of 82 is 0.9496776978825432 =======================================
The Arc Cosine of an Angle
Imagine you have an angle named u in a right triangle. To calculate the value v of the cosine of that angle, you would write:
v = cosin(u)
To let you consider the opposite of a cosine, trigonometry provides the concept of an arc cosine. In trigonometry, it is written arccos. To get the opposite of the cosine of the angle, you would write:
u = arccos(v)
To support arc cosines, the Matt class provides a function named Acos. Its syntax is:
public static double Acos (double d);
To calculate the arc cosine of a value, pass a number to the function. The number must be between -1 and 1. Here is an example:
@page
@model Valuable.Pages.CreatureModel
@{
double number = .426;
double cosine = Math.Cos(number);
double arcosine = Math.Acos(number);
}
<pre>=============================================
The cosine of @number is @cosine
The arc cosine of @number is @arcosine
=============================================</pre>
This would produce:
============================================= The cosine of 0.426 is 0.9106259567216819 The arc cosine of 0.426 is 1.1307294179513676 ==============================================
![]() Practical Learning: Introducing Cosines
Practical Learning: Introducing Cosines
@page
@model ObliqueTriangles1.Pages.SASModel
@{
string? strMessage = null;
double side1 = 0.00, side2 = 0.00, side3 = 0.00;
double angle1 = 0.00, angle2 = 0.00, angle3 = 0.00;
if (Request.HasFormContentType)
{
try
{
side1 = double.Parse(Request.Form["txtSASSide1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for one of the known sides of the SAS shape.";
}
try
{
angle1 = double.Parse(Request.Form["txtSASAngle1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the known angle of the SAS shape.";
}
try
{
side2 = double.Parse(Request.Form["txtSASSide2"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the other known side of the SAS shape.";
}
// Here, we use the law of cosines
side3 = Math.Sqrt((side1 * side1) +
(side2 * side2) -
(2 * side1 * side2 * Math.Cos(angle1 * Math.PI / 180)));
angle2 = Math.Acos(((side3 * side3) +
(side2 * side2) -
(side1 * side1)) /
(2 * side3 * side2)) * 180 / Math.PI;
angle3 = 180 - (angle1 + angle2);
}
}
<div class="delimiter common-font">
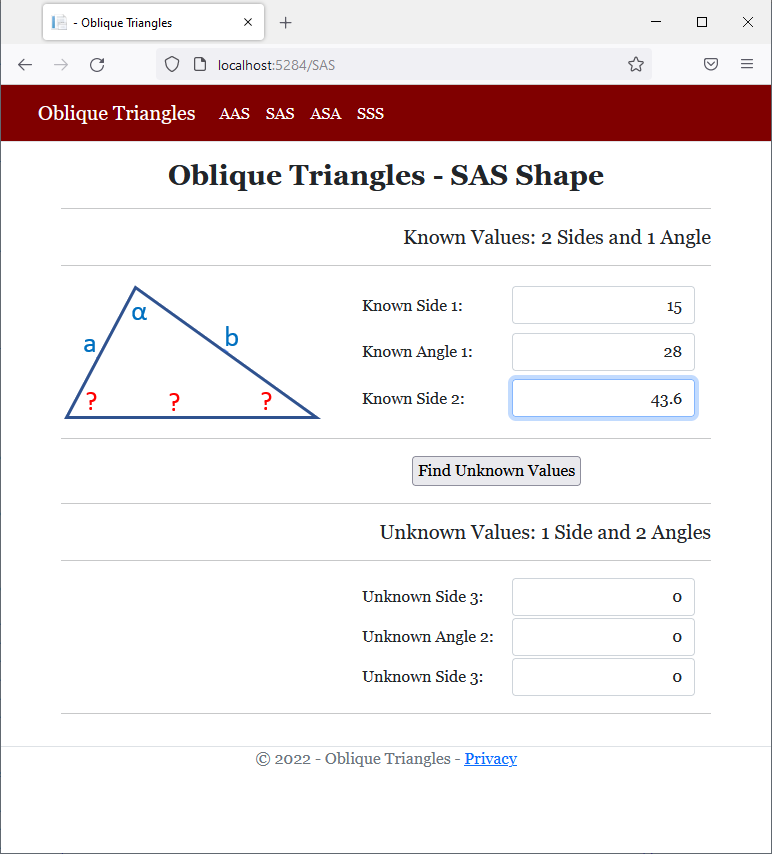
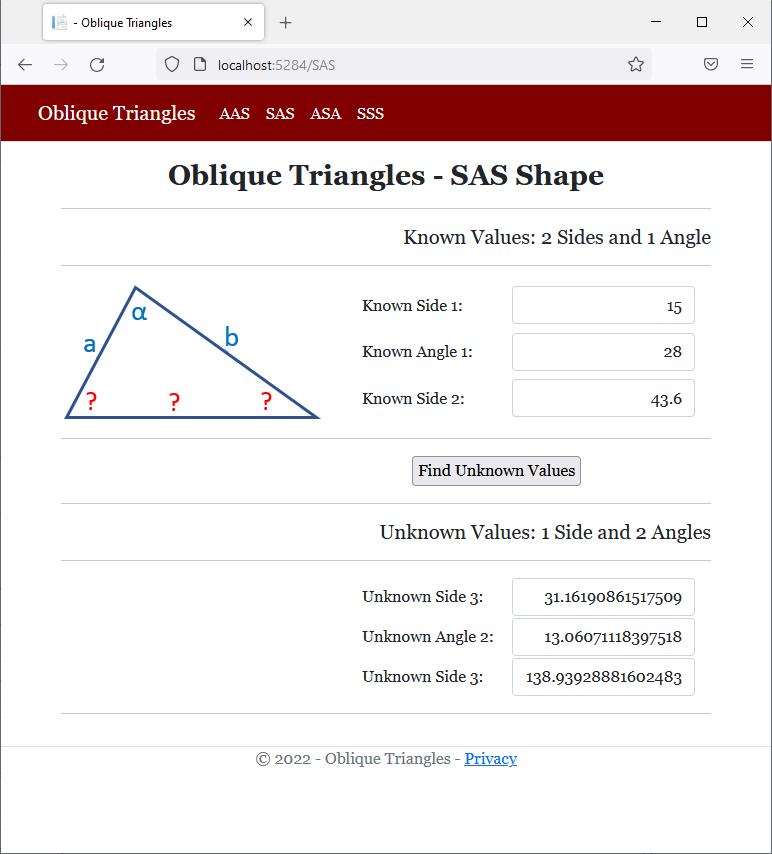
<h2 class="text-center bold">Oblique Triangles - SAS Shape</h2>
<hr />
<h5 class="text-right">Known Values: 2 Sides and 1 Angle</h5>
<hr />
<form name="frmGeometry" method="post">
<table>
<tr>
<td style="width: 300px" rowspan="3">
<img src="~/images/sas.png" width="260" height="138" alt="Oblique Triangles - SAS Shape">
</td>
<td style="width: 150px">Known Side 1:</td>
<td>@Html.TextBox("txtSASSide1", @side1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Angle 1:</td>
<td>@Html.TextBox("txtSASAngle1", @angle1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 2:</td>
<td>@Html.TextBox("txtSASSide2", @side2, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<table>
<tr>
<td style="width: 350px"> </td>
<td style="text-align: center"><input type="submit" name="btnSubmit" value="Find Unknown Values" /></td>
</tr>
</table>
</form>
<hr />
<h5 class="text-right">Unknown Values: 1 Side and 2 Angles</h5>
<hr />
<table>
<tr>
<td style="width: 300px"> </td>
<td style="width: 150px">Unknown Angle 2:</td>
<td>@Html.TextBox("txtSASAngle2", @angle2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Side 3:</td>
<td>@Html.TextBox("txtSASSide3", @side3, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Angle 3:</td>
<td>@Html.TextBox("txtSASAngle3", @angle3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<p class="text-center">@strMessage</p>
</div>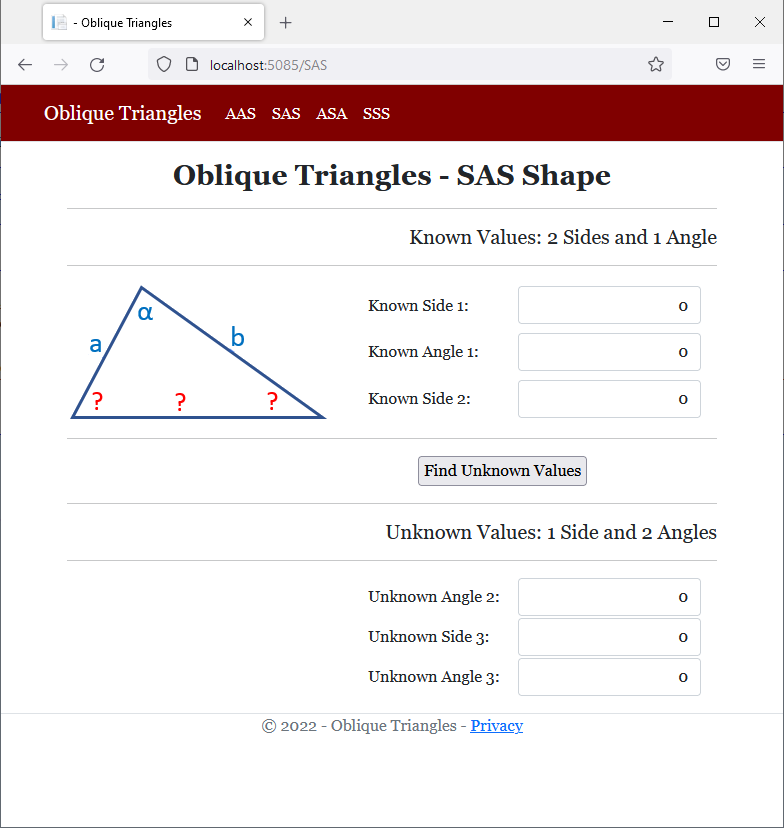
@page
@model ObliqueTriangles1.Pages.ASAModel
@{
string? strMessage = null;
double side1 = 0.00, side2 = 0.00, side3 = 0.00;
double angle1 = 0.00, angle2 = 0.00, angle3 = 0.00;
if (Request.HasFormContentType)
{
try
{
angle1 = double.Parse(Request.Form["txtASAAngle1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for one of the known angles of the ASA shape.";
}
try
{
side1 = double.Parse(Request.Form["txtASASide1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the side that is between the angles whose values are about the ASA shape.";
}
try
{
angle2 = double.Parse(Request.Form["txtASAAngle2"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the other known angle of the ASA oblique triangle.";
}
// Here, we use the law of sines
angle3 = 180 - (angle1 + angle2);
side2 = side1 * Math.Sin(angle2 * Math.PI / 180) / Math.Sin(angle1 * Math.PI / 180);
side3 = side1 * Math.Sin(angle3 * Math.PI / 180) / Math.Sin(angle1 * Math.PI / 180);
}
}
<div class="delimiter common-font">
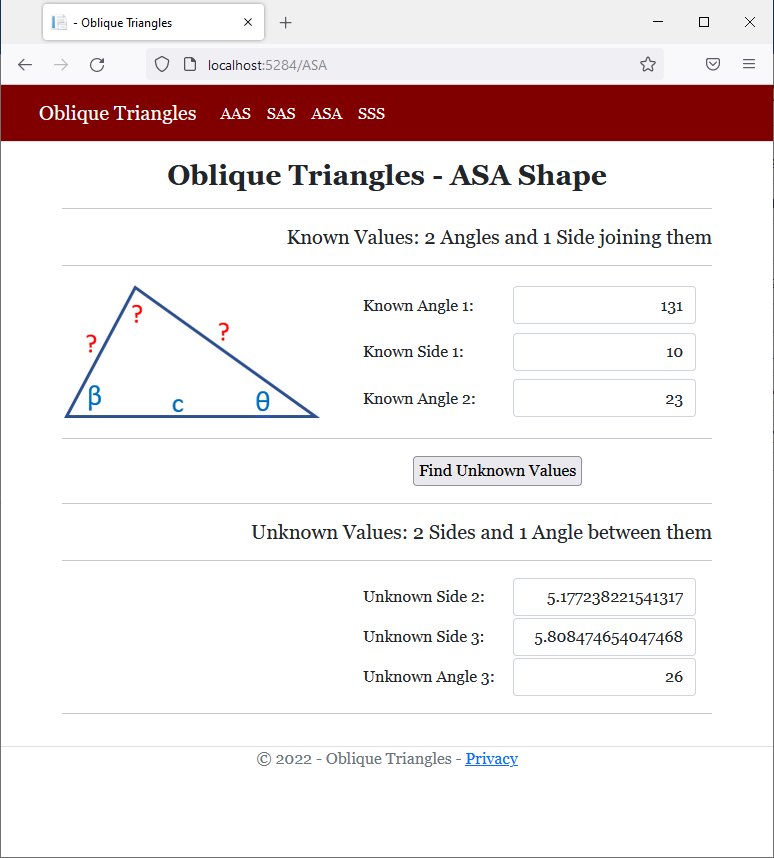
<h2 class="text-center bold">Oblique Triangles - ASA Shape</h2>
<hr />
<h5 class="text-right">Known Values: 2 Angles and 1 Side joining them</h5>
<hr />
<form name="frmGeometry" method="post">
<table>
<tr>
<td style="width: 300px" rowspan="3">
<img src="~/images/asa.png" width="260" height="138" alt="Oblique Triangles - SAS Shape">
</td>
<td style="width: 150px">Known Angle 1:</td>
<td>@Html.TextBox("txtASAAngle1", @angle1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 1:</td>
<td>@Html.TextBox("txtASASide1", @side1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Angle 2:</td>
<td>@Html.TextBox("txtASAAngle2", @angle2, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<table>
<tr>
<td style="width: 350px"> </td>
<td style="text-align: center"><input type="submit" name="btnSubmit" value="Find Unknown Values" /></td>
</tr>
</table>
</form>
<hr />
<h5 class="text-right">Unknown Values: 2 Sides and 1 Angle between them</h5>
<hr />
<table>
<tr>
<td style="width: 300px"> </td>
<td style="width: 150px">Unknown Side 2:</td>
<td>@Html.TextBox("txtASASide2", @side2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Angle 3:</td>
<td>@Html.TextBox("txtASAAngle3", @angle3, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Side 3:</td>
<td>@Html.TextBox("txtASASide3", @side3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<p class="text-center">@strMessage</p>
</div>@page
@model ObliqueTriangles1.Pages.SSSModel
@{
string? strMessage = null;
double side1 = 0.00, side2 = 0.00, side3 = 0.00;
double angle1 = 0.00, angle2 = 0.00, angle3 = 0.00;
if (Request.HasFormContentType)
{
try
{
side1 = double.Parse(Request.Form["txtSSSSide1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for one of the known sides of the SSS shape.";
}
try
{
side2 = double.Parse(Request.Form["txtSSSSide2"]);
}
catch (FormatException)
{
strMessage = "You must type a value for another side of the SSS triangle.";
}
try
{
side3 = double.Parse(Request.Form["txtSSSSide3"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the remaining known side of the SSS oblique triangle.";
}
// Here, we use the law of cosines
angle1 = Math.Acos(((side3 * side3) +
(side2 * side2) -
(side1 * side1)) /
(2 * side3 * side2)) * 180 / Math.PI;
angle2 = Math.Acos(((side3 * side3) +
(side1 * side1) -
(side2 * side2)) /
(2 * side3 * side1)) * 180 / Math.PI;
angle3 = 180 - (angle1 + angle2);
}
}
<div class="delimiter common-font">
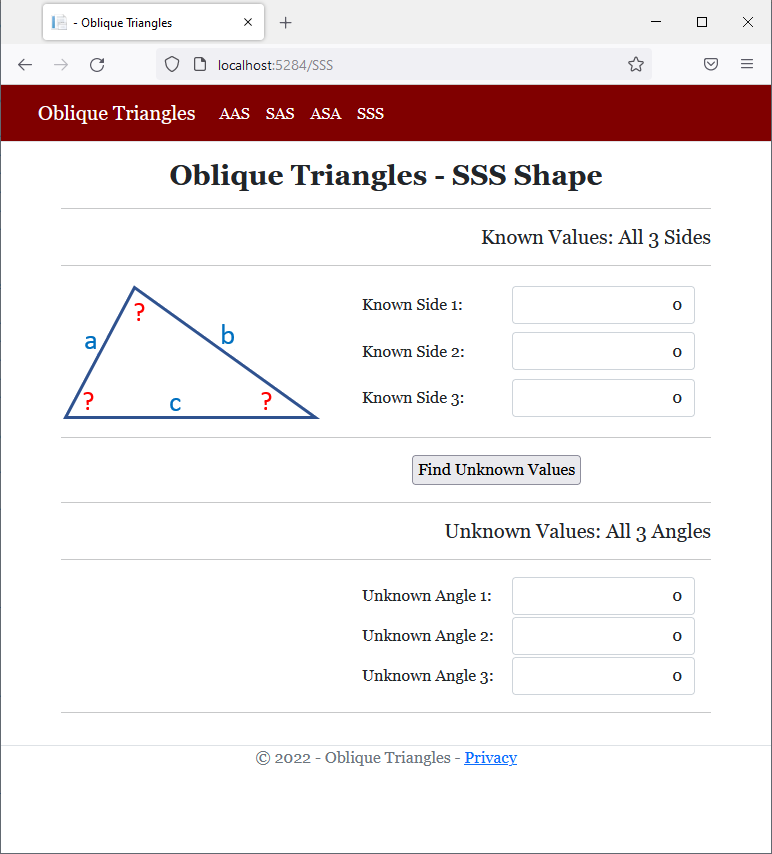
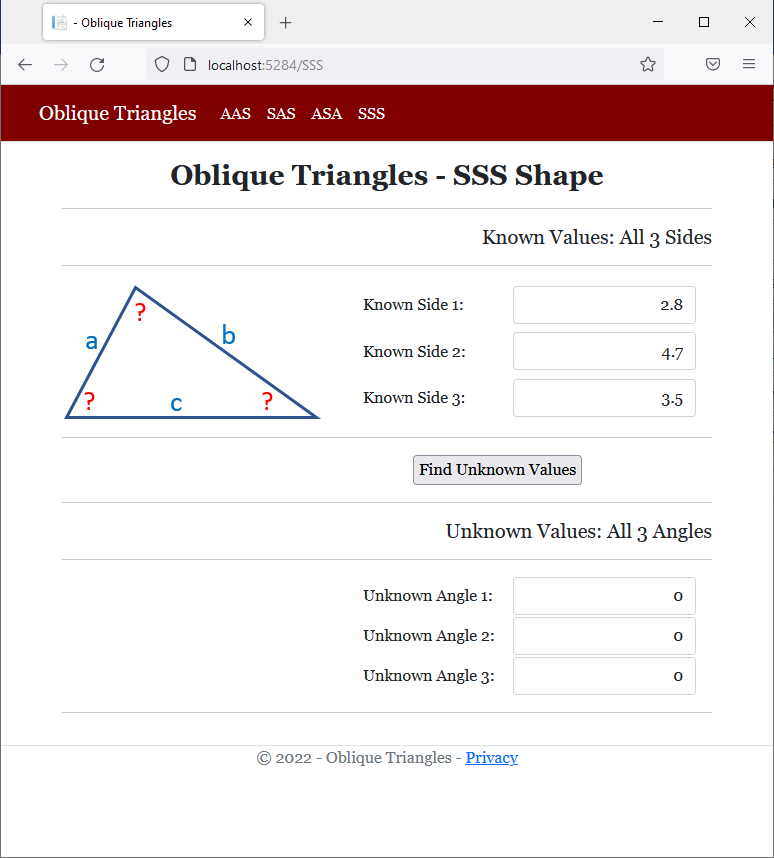
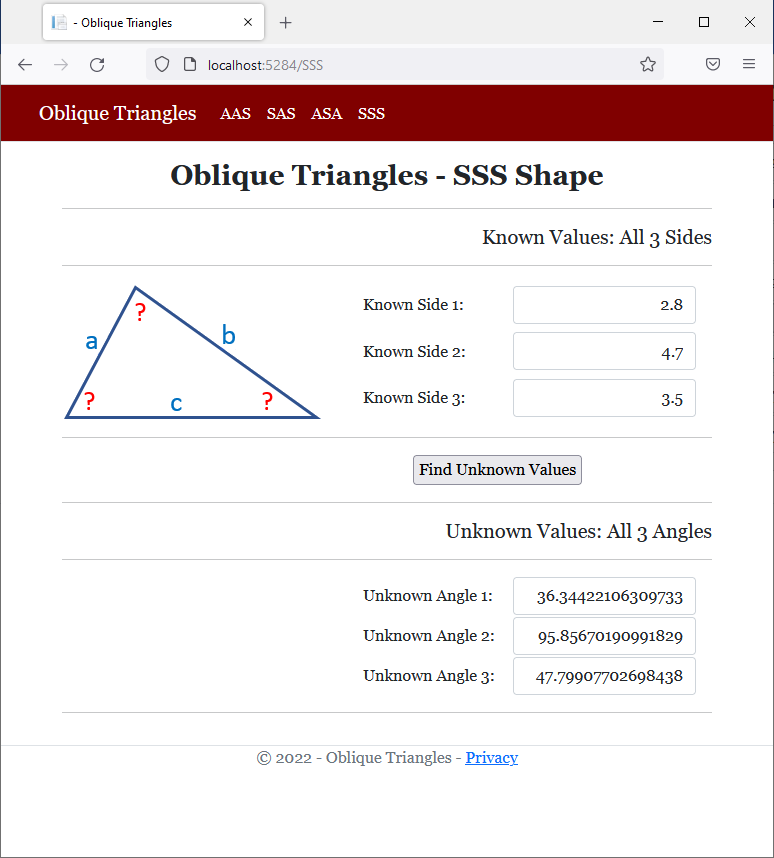
<h2 class="text-center bold">Oblique Triangles - SSS Shape</h2>
<hr />
<h5 class="text-right">Known Values: All 3 Sides</h5>
<hr />
<form name="frmGeometry" method="post">
<table>
<tr>
<td style="width: 300px" rowspan="3">
<img src="~/images/sss.png" width="259" height="137" alt="Oblique Triangles - SSS Shape">
</td>
<td style="width: 150px">Known Side 1:</td>
<td>@Html.TextBox("txtSSSSide1", @side1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 2:</td>
<td>@Html.TextBox("txtSSSSide2", @side2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 3:</td>
<td>@Html.TextBox("txtSSSSide3", @side3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<table>
<tr>
<td style="width: 350px"> </td>
<td style="text-align: center"><input type="submit" name="btnSubmit" value="Find Unknown Values" /></td>
</tr>
</table>
</form>
<hr />
<h5 class="text-right">Unknown Values: All 3 Angles</h5>
<hr />
<table>
<tr>
<td style="width: 300px"> </td>
<td style="width: 150px">Unknown Angle 1:</td>
<td>@Html.TextBox("txtSSSAngle1", @angle1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Angle 2:</td>
<td>@Html.TextBox("txtSSSAngle2", @angle2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Angle 3:</td>
<td>@Html.TextBox("txtSSSAngle3", @angle3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<p class="text-center">@strMessage</p>
</div>

Tangents
Consider AC the length of A to C. Also consider BC the length of B to C. The tangent is the result of BC/AC; that is, the ratio of BC over AC. To assist you with calculating the tangent of of a number, the Math class is equipped with a method named Tan whose syntax is:
public static double Tan(double a);
Here is an example that calls this function:
@page
@model Valuable.Pages.CreatureModel
@{
double number = 42.6;
double tangent = Math.Tan(number);
}
<pre>=============================================
The tangent of @number is @tangent
=============================================</pre>
FutureValue
============================================= The tangent of 42.6 is -5.2420805599568565 =============================================
The Arc Tangent
Consider BC the length of B to C. Also consider AC the length of A to C. The arc tangent is the ratio of BC/AC. To calculate the arc tangent of a value, you can use the Math.Atan()method. Its syntax is
public static double Atan(double d);
Here is an example:
@page
@model Valuable.Pages.CreatureModel
@{
double number = 42.6;
double tangent = Math.Tan(number);
double arctangent = Math.Atan(number);
}
<pre>=============================================
The tangent of @number is @tangent
The arc tangent of @number is @arctangent
=============================================</pre>
This would produce:
============================================= The tangent of 42.6 is -5.2420805599568565 The arc tangent of 42.6 is 1.547326458680173 =============================================
![]() Practical Learning: Ending the Lesson
Practical Learning: Ending the Lesson
|
|
|||
| Previous | Copyright © 2001-2022, FunctionX | Tuesday 08 February 2022 | Next |
|
|
|||