Characteristics of Values Types
Characteristics of Values Types
A Double-Word
Introduction
A double-word is a group of two consecutive Words. This means that a double-word combines 4 bytes or 32 bits. The minimum binary number you can represent with a double-word is 0. The minimum decimal value of a double-word is 0. To find out the maximum decimal value of a word, you can use the base 2 formula giving a 1 value to each bit:
| 2n-1 | 230 | 229 | 228 | 227 | 226 | 225 | 224 |
| etc | 1,073,741,824 | 536,870,912 | 268,435,456 | 134,217,728 | 67,108,864 | 33,554,432 | 16,777,216 |
| 223 | 222 | 221 | 220 | 219 | 218 | 217 | 216 |
| 8,388,608 | 4,194,304 | 2,097,152 | 1,048,576 | 524,288 | 262,144 | 131,072 | 65,536 |
| 215 | 214 | 213 | 212 | 211 | 210 | 29 | 28 |
| 32,768 | 16,384 | 8,192 | 4,096 | 2,048 | 1,024 | 512 | 256 |
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
1*231+1*230+1*229 + 1*228 + 1*227 + 1*226 + 1*225 + 1*224 + 1*223 + 1*222 + 1*221 + 1*220 + 1*219 + 1*218 + 1*217 + 1*216 + 1*215 + 1*214 + 1*213 + 1*212 + 1*211 + 1*210 + 1*29 + 1*28 + 1*27 + 1*26 + 1*25 + 1*24 + 1*23 + 1*22 + 1*21 + 1*20
= 2,147,483,648 + 1,073,741,824 + 536,870,912 + 268,435,456 + 134,217,728 + 67,108,864 + 33,554,432 + 16,777,216 + 8,388,608 + 4,194,304 + 2,097,152 + 1,048,576 + 524,288 + 262,144 + 131,072 + 65,536 + 32,768 + 16,384 + 8,192 + 4,096 + 2,048 + 1,024 + 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1
= 4,286,578,708
The minimum hexadecimal value you can store in a double-word is 0x00000000000000000000000000000000 which is the same as 0x0. To find out the maximum hexadecimal number you can represent with a word, replace every group of 4-bits with an f or F:
| 1111 | 1111 | 1111 | 1111 | 1111 | 1111 | 1111 | 1111 |
| f | f | f | f | f | f | f | f |
| = 0xffffffff = 0xFFFFFFFF | |||||||
To declare a variable that can hold large values, you can use the var keyword and initialize the variable with the desired value. Here is an example:
@page
@model Exercises.Pages.ExerciseModel
@{
var apartNbr = 24;
}
<pre>===============================
Apartment Rental Management
-------------------------------
Apartment #: @apartNbr);
===============================>/pre>
This would produce:
=============================== Apartment Rental Management ------------------------------- Apartment #: 24 ===============================
A double-word is large enough to contain double the amount of data that can be stored in a word. This is equivalent to 32 bits or 4 bytes or 4,294,967,295. Therefore, a double-word is used for small or large numbers.
To use a variable that would hold quite large numbers, besides the var keyword, you can declare it using the int keyword. A variable declared as int can store values between -2,147,483,648 and 2,147,484,647 negative or positive, that can fit in 32 bits. Here are examples of variables declared as integers:
@page
@model Exercises.Pages.ExerciseModel
@{
int coordX = 12;
int coordY = -8;
}
<pre>=======================================
Cartesian Coordinate System: P(@coordX, @coordY)
=======================================</pre>
When executed, the program would produce:
======================================= Cartesian Coordinate System: P(12, -8) =======================================
If the number is large, don't use the character for thousands separators, which in English is the comma used in the English language. Here is an example:
@page
@model Exercises.Pages.ExerciseModel
@{
int yearlySalary = 82460;
}
<pre>=======================================
Fun Department Store
Yearly Salary: @yearlySalary
=======================================</pre>
The program would produce:
======================================= Fun Department Store Yearly Salary: 82460 =======================================
Characteristics of Integers
Creating an Integral Value
As mentioned already, an integer is a combination of digits to represent a natural number. By default, when creating the number in a C# application, use only digits. Still, if the number is large or very large and becomes difficult to read, you can separate the thousands from right to left with underscores. Here are examples:
@page
@model Exercises.Pages.ExerciseModel
@{
var emplNbr = 20_931_705;
int yearlySalary = 82_460;
}
<pre>==========================
Fun Department Store
--------------------------
Employee #: @emplNbr
Yearly Salary: @yearlySalary
==========================</pre>
This would produce:
========================== Fun Department Store -------------------------- Employee #: 20931705 Yearly Salary: 82460 ==========================
Declaring a Variant Integral Variable
If you declare an integer variable using the var keyword and initialize it with a value lower than 2,147,484,647, the compiler concludes that the memory needed to store that variable is 32 bits:
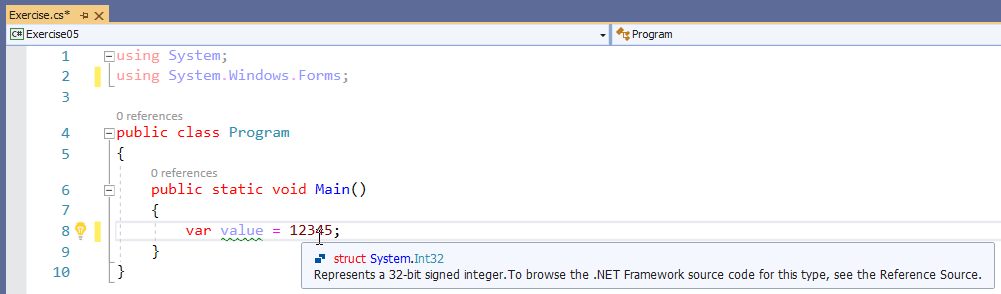
Hexadecimal Numbers
When initializing an integral variable, instead of a decimal number, you can also initialize it with a hexadecimal value whose decimal equivalent is less than 2,147,484,647. Here is an example:
@page
@model Exercises.Pages.ExerciseModel
@{
var number = 0xF0488EA;
}
<pre>==========================
Number: @number
==========================>/pre>
This would produce:
========================== Number: 251955434 ==========================
Remember that you can declare the variable using the int, the var, or the dynamic keyword. In this case, initialize the variable with a natural number Here are examples:
@{
int score = 3907;
var feel = 95;
dynamic face = 794800;
A 32-Bit Integer
To support 32-bit integers, the .NET library provides a structure named Int32. You can use it to declare a variable. Here is an example:
@{
int score = 3907;
var feel = 95;
dynamic face = 794800;
Int32 ambiance = 9284;
}
The .NET library represents the int data type with a structure named Int32.
The Int32 just like the int data type are for variables that can hold values between -2,147,483,648 and 2,147,483,647. The Int32 structure is equipped with fields and methods that use the exact same names we reviewed for the byte type. This includes the ability to parse a value et get a converted integer. That structure also allows you to get the minimum and the maximum values of a 32-bit variable. Here are examples:
@page
@model Exercises.Pages.ExerciseModel
@{
}
<pre>=====================================
byte integer minimum: @byte.MinValue
Byte integer minimum: @Byte.MinValue
-------------------------------------
byte integer maximum: @byte.MaxValue
Byte integer maximum: @Byte.MaxValue
=====================================
Short integer minimum: @short.MinValue
16-bit integer minimum: @Int16.MinValue
-------------------------------------
Short integer maximum: @short.MaxValue
16-bit integer maximum: @Int16.MaxValue
=====================================
Unsigned short minimum: @ushort.MinValue
Unsigned short maximum: @ushort.MaxValue
-------------------------------------
Integer minimum: @int.MinValue
Int32 minimum: @Int32.MinValue
-------------------------------------"
Integer maximum: @int.MaxValue
Int32 maximum: @Int32.MaxValue
=====================================</pre>
This would produce:
===================================== byte integer minimum: 0 Byte integer minimum: 0 ------------------------------------- byte integer maximum: 255 Byte integer maximum: 255 ===================================== Short integer minimum: -32768 16-bit integer minimum: -32768 ------------------------------------- Short integer maximum: 32767 16-bit integer maximum: 32767 ===================================== Unsigned short minimum: 0 Unsigned short maximum: 65535 ------------------------------------- Integer minimum: -2147483648 Int32 minimum: -2147483648 ------------------------------------- Integer maximum: 2147483647 Int32 maximum: 2147483647 =====================================
Converting a Value to an Integer
While the Int32 structure is equipped to parse a value and get an integral value, the static Convert class is equipped with an overloaded method that can be used to convert a value to an integer. To let you convert a value to an integer, the Convert class provides an overloaded method named to ToInt32. If the value to convert is a string, such as one of the values the user would type in, or select from, a Windows controller, use the following version:
public static int ToInt32 (string value);
The method is also equipped to consider any other type. Therefore, based on the data types we have seen so far, you can use one of the following versions of the method:
public static int ToInt32 (byte value); public static int ToInt32 (short value);
If you don't know the type of the value you want to convert, the class offers the following version of the method:
public static int ToInt32 (object value);
In either case, pass the desired value to the method. If the method succeeds with the conversion, it would produce the integral format of the argument.
An unsigned integer is a positive natural number that can fit in up to 32 bits of the computer memory. To let you declare a variable for such a number, the C# language provides a data type named uint. The uint keyword is used for a 32-bit positive integer that is between 0 and 4,294,967,295. Here are examples of unsigned integer types:
@page
@model Exercises.Pages.ExerciseModel
@{
uint dayOfBirth = 8;
uint monthOfBirth = 11;
uint yearOfBirth = 2022;
}
<pre>==================================
Red Oak High School
Student Date of Birth: @monthOfBirth/@dayOfBirth/@yearOfBirth
==================================</pre>
This would produce:
================================== Red Oak High School Student Date of Birth: 11/8/2022 ==================================
Once again, if the number is large, you can use the underscore to separate the thousands.
Operations on Integers
Integers support all of the four regular operations: addition, subtraction, multiplication, and division. When it comes to the division:
@page
@model Exercises.Pages.ExerciseModel
@{
}
<pre>Operation 1000 / 240 = @1000 / 240
--------------------------
Operation 1226 / 317 = @1226 / 317
==========================</pre>
This would produce:
Operation 1000 / 240 = 4 -------------------------- Operation 1226 / 317 = 3 ==========================
Introduction
To store a very large number that cannot fit in a double-word, you can consider a combination of 64 bits. The group can also be referred to as a quad-word. A quad-word is very large. It can store numbers in the range of -9,223,372,036,854,775,808 and 9,223,372,036,854,775,807.
If you declare an integer variable using the var keyword and initialize it with a value between 2,147,484,647 and 9,223,372,036,854,775,807, the compiler concludes that the memory needed to store that variable is 64 bits:
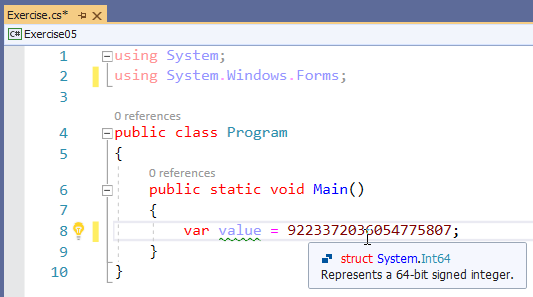
To let you use a variable that can hold very large numbers that may require up to 64 bits, the C# language provides a data type named long. You can use it to declare a variable. Here is an example of a variable of a long integer type:
@page
@model Exercises.Pages.ExerciseModel
@{
long areaSqrMiles = 3705407;
}
<pre>Country Statistics
Area: @areaSqrMiles Sqr Miles
==========================</pre>
This would produce:
Country Statistics Area: 3705407 Sqr Miles ==========================
As always, you can also use the var keyword to declare the variable. When initializing the variable, don't use the official thousands separator. Instead, you can either type the number as it is or you can use the underscore(s) to separate the thousands. Here are examples:
@page
@model Exercises.Pages.ExerciseModel
@{
long areaSqrMiles = 3705407;
long areaSqrKms = 9_596_961;
long population = 1_403_500_365;
}
<pre>Country Statistics
------------------------------------------------
Area: @areaSqrKms Sqr Kms (@areaSqrMiles Sqr Miles)
Population: @population
================================================</pre>
This would produce:
Country Statistics ------------------------------------------------ Area: 9596961 Sqr Kms (3705407 Sqr Miles) Population: 1403500365 ================================================
As stated previously, if you initialize the variable with a value lower than 2,147,484,647, the compiler would allocate 32 bits of memory for it. If you initialize the variable with a value between 2,147,484,647 and 9,223,372,036,854,775,807, the compiler would allocate 64 bits of memory for it. If the value is higher than 9,223,372,036,854,775,807, which is too large, the compiler would present an error.
This means that you should limit the values assigned to integral variables to 64 bits, which is very significant. Here is an example:
@page
@model Exercises.Pages.ExerciseModel
@{
var countryArea = 5638648;
}
<pre>Country Statistics
------------------------------------------------
Country Area: @countryArea km2
================================================</pre>
This would produce:
Country Statistics ------------------------------------------------ Country Area: 5638648 km2 ================================================
As mentioned for other integral types, you can initialize a long variable with a hexadecimal value.
Although the long data type is used for large numbers, it mainly indicates the amount of space available but you don't have to use the whole space. For example, you can use the long keyword to declare a variable that would hold the same range of numbers as the short, the int, or the uint data types. If you declare a variable as long but use it for small numbers that don't require 64 bits, the compiler would allocate the appropriate amount of space to accommodate the values of the variable. Consequently, the amount of space made available may not be as large as 64 bits. If you insist and want the compiler to reserve 64 bits, when assigning a value to the variable, add an L suffix to it. Here is an example that uses a long variable to store a number that would fit in 32 bits:
@{
long countryArea = 5638648L;
}
<pre>Country Area: @countryArea km2
========================================</pre>
This would produce:
Country Area: 5638648 km2 ========================================
Therefore, keep in mind that an int, a uint, ashort, or a ushort can fit in a long variable.
.NET Long Integers
To support long integers, the .NET library provides a structure named Int64. That structure holds the characteristics of the long data type. Here are examples of accessing the minimum and the maximum values:
@page
@model Exercises.Pages.ExerciseModel
@{
}
<pre>===========================================================================
Byte Minimum Value (Natural): @byte.MinValue.ToString()
Byte Minimum Value (Hexadecimal): 0x@(byte.MinValue.ToString("X"))
Byte Maximum Value (Natural): @Byte.MaxValue.ToString()
Byte Maximum Value (Hexadecimal): 0x@(Byte.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Short Minimum Value (Natural): @short.MinValue.ToString()
Short Minimum Value (Natural): @short.MinValue.ToString("X")
Short Maximum Value (Natural): @Int16.MaxValue.ToString()
Short Maximum Value (Hexadecimal): 0x@(Int16.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Unsigned Short Minimum Value (Natural): @ushort.MinValue.ToString()
Unsigned Short Minimum Value (Natural): @ushort.MinValue.ToString("X")
Unsigned Short Maximum Value (Natural): @ushort.MaxValue.ToString()
Unsigned Short Value (Hexadecimal): 0x@(ushort.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Integer Minimum Value (Natural): @Int32.MinValue.ToString("N")
Integer Minimum Value (Hexadecimal): 0x@(Int32.MinValue.ToString("X"))
Integer Maximum Value (Natural): @Int32.MaxValue.ToString("N")
Integer Maximum Value (Hexadecimal): 0x@(Int32.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Unsigned Integer Minimum Value (Natural): @uint.MinValue.ToString()
Unsigned Integer Minimum Value (Hexadecimal): 0x@(uint.MinValue.ToString("X"))
Unsigned Integer Maximum Value (Natural): @uint.MaxValue.ToString("N")
Unsigned Integer Value (Hexadecimal): 0x@(uint.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Long Minimum Value (Natural): @long.MinValue.ToString("N")
Long Minimum Value (Hexadecimal): 0x@(long.MinValue.ToString("X"))
Long Maximum Value (Natural): @long.MaxValue.ToString("N")
Long Maximum Value (Hexadecimal): 0x@(long.MaxValue.ToString("X"))
============================================================================</pre>
This would produce:
=========================================================================== Byte Minimum Value (Natural): 0 Byte Minimum Value (Hexadecimal): 0x0 Byte Maximum Value (Natural): 255 Byte Maximum Value (Hexadecimal): 0xFF ---------------------------------------------------------------------------- Short Minimum Value (Natural): -32768 Short Minimum Value (Natural): 8000 Short Maximum Value (Natural): 32767 Short Maximum Value (Hexadecimal): 0x7FFF ---------------------------------------------------------------------------- Unsigned Short Minimum Value (Natural): 0 Unsigned Short Minimum Value (Natural): 0 Unsigned Short Maximum Value (Natural): 65535 Unsigned Short Value (Hexadecimal): 0xFFFF ---------------------------------------------------------------------------- Integer Minimum Value (Natural): -2,147,483,648.00 Integer Minimum Value (Hexadecimal): 0x80000000 Integer Maximum Value (Natural): 2,147,483,647.00 Integer Maximum Value (Hexadecimal): 0x7FFFFFFF ---------------------------------------------------------------------------- Unsigned Integer Minimum Value (Natural): 0 Unsigned Integer Minimum Value (Hexadecimal): 0x0 Unsigned Integer Maximum Value (Natural): 4,294,967,295.00 Unsigned Integer Value (Hexadecimal): 0xFFFFFFFF ---------------------------------------------------------------------------- Long Minimum Value (Natural): -9,223,372,036,854,775,808.00 Long Minimum Value (Hexadecimal): 0x8000000000000000 Long Maximum Value (Natural): 9,223,372,036,854,775,807.00 Long Maximum Value (Hexadecimal): 0x7FFFFFFFFFFFFFFF ============================================================================
You can use a combination of 64 bits to store positive or negative integers. In some cases, you will need a variable to hold only positive, though large, numbers. To declare such a variable, you can use the ulong data type. A variable declared as ulong can handle extremely positive numbers that range from 0 to 18,446,744,073,709,551,615 to fit in 64 bits. Here is an example of accessing the minimum and the maximum values of an unsigned long integer:
@page
@model Exercises.Pages.ExerciseModel
@{
}
<pre>===========================================================================
Byte Minimum Value (Natural): @byte.MinValue.ToString()
Byte Minimum Value (Hexadecimal): 0x@(byte.MinValue.ToString("X"))
Byte Maximum Value (Natural): @Byte.MaxValue.ToString()
Byte Maximum Value (Hexadecimal): 0x@(Byte.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Short Minimum Value (Natural): @short.MinValue.ToString()
Short Minimum Value (Natural): @short.MinValue.ToString("X")
Short Maximum Value (Natural): @Int16.MaxValue.ToString()
Short Maximum Value (Hexadecimal): 0x@(Int16.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Unsigned Short Minimum Value (Natural): @ushort.MinValue.ToString()
Unsigned Short Minimum Value (Natural): @ushort.MinValue.ToString("X")
Unsigned Short Maximum Value (Natural): @ushort.MaxValue.ToString()
Unsigned Short Value (Hexadecimal): 0x@(ushort.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Integer Minimum Value (Natural): @Int32.MinValue.ToString("N")
Integer Minimum Value (Hexadecimal): 0x@(Int32.MinValue.ToString("X"))
Integer Maximum Value (Natural): @Int32.MaxValue.ToString("N")
Integer Maximum Value (Hexadecimal): 0x@(Int32.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Unsigned Integer Minimum Value (Natural): @uint.MinValue.ToString()
Unsigned Integer Minimum Value (Hexadecimal): 0x@(uint.MinValue.ToString("X"))
Unsigned Integer Maximum Value (Natural): @uint.MaxValue.ToString("N")
Unsigned Integer Value (Hexadecimal): 0x@(uint.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Long Minimum Value (Natural): @long.MinValue.ToString("N")
Long Minimum Value (Hexadecimal): 0x@(long.MinValue.ToString("X"))
Long Maximum Value (Natural): @long.MaxValue.ToString("N")
Long Maximum Value (Hexadecimal): 0x@(long.MaxValue.ToString("X"))
----------------------------------------------------------------------------
Unsigned Long Minimum Value (Natural): @ulong.MinValue.ToString("N")
Unsigned Long Minimum Value (Hexadecimal): 0x@(ulong.MinValue.ToString("X"))
Unsigned Long Maximum Value (Natural): @ulong.MaxValue.ToString("N")
Unsigned Long Maximum Value (Hexadecimal): 0x@(ulong.MaxValue.ToString("X"))
============================================================================</pre>
This would produce:
=========================================================================== Byte Minimum Value (Natural): 0 Byte Minimum Value (Hexadecimal): 0x0 Byte Maximum Value (Natural): 255 Byte Maximum Value (Hexadecimal): 0xFF ---------------------------------------------------------------------------- Short Minimum Value (Natural): -32768 Short Minimum Value (Natural): 8000 Short Maximum Value (Natural): 32767 Short Maximum Value (Hexadecimal): 0x7FFF ---------------------------------------------------------------------------- Unsigned Short Minimum Value (Natural): 0 Unsigned Short Minimum Value (Natural): 0 Unsigned Short Maximum Value (Natural): 65535 Unsigned Short Value (Hexadecimal): 0xFFFF ---------------------------------------------------------------------------- Integer Minimum Value (Natural): -2,147,483,648.00 Integer Minimum Value (Hexadecimal): 0x80000000 Integer Maximum Value (Natural): 2,147,483,647.00 Integer Maximum Value (Hexadecimal): 0x7FFFFFFF ---------------------------------------------------------------------------- Unsigned Integer Minimum Value (Natural): 0 Unsigned Integer Minimum Value (Hexadecimal): 0x0 Unsigned Integer Maximum Value (Natural): 4,294,967,295.00 Unsigned Integer Value (Hexadecimal): 0xFFFFFFFF ---------------------------------------------------------------------------- Long Minimum Value (Natural): -9,223,372,036,854,775,808.00 Long Minimum Value (Hexadecimal): 0x8000000000000000 Long Maximum Value (Natural): 9,223,372,036,854,775,807.00 Long Maximum Value (Hexadecimal): 0x7FFFFFFFFFFFFFFF ---------------------------------------------------------------------------- Unsigned Long Minimum Value (Natural): 0.00 Unsigned Long Minimum Value (Hexadecimal): 0x0 Unsigned Long Maximum Value (Natural): 18,446,744,073,709,551,615.00 Unsigned Long Maximum Value (Hexadecimal): 0xFFFFFFFFFFFFFFFF ============================================================================
Floating-Point Numbers
Introduction to Real Numbers
A real number is a number that displays a decimal part. This means that the number can be made of two sections separated by a symbol that is referred to as the Decimal Separator or Decimal Symbol. This symbol is different by language, country, group of languages, or group of countries. In US English, this symbol is the period as can be verified from the Regional (and Language) Settings of the Control Panel:
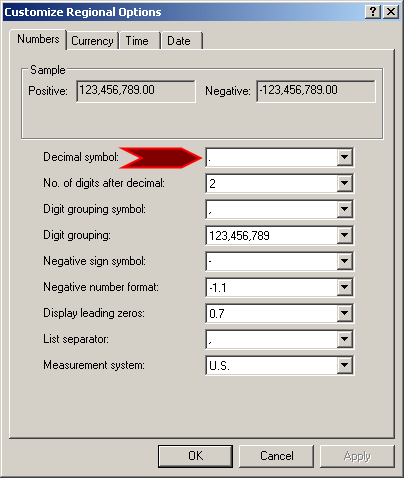
On both sides of the decimal symbol, digits are used to specify the value of the number. The number of digits on the right side of the symbol determines how much precision the number offers.
Introduction to Floating-Point Numbers
The most fundamental data type you can use for a floating-point number is called float. A variable declared as float can store real numbers that range from 3.402823e38 to 3.402823e38 in 32 bits. Here is an example:
@{
float distance;
}
A Number with Single-Precision
As seen with integers, to support real numbers, the .NET library provides various structures. All the structures are created in the System namespace.
To support numbers with single-precision, the .NET library provides a structure named Single. The Single structure is used to support the float data type of the C# language. This means that the characteristics of the float data type are defined in the Single structure. All the characteristics we reviewed for the structures associated with integers are also available for real numbers. This includes the ability to display a value by calling one of the versions of the overloaded ToString() methods that every number-associated structure is equipped with. The operations also include the ability to parse or to to try parsing a value to produce an appropriate real number.
![]() Practical Learning: Introducing Real Numbers
Practical Learning: Introducing Real Numbers
body {
}
.bold { font-weight: bold; }
.text-right { text-align: right }
.delimiter { margin: auto;
width: 650px; }
.top-bar { border-bottom: 6px solid blue;
background-color: #800000 !important; }
.common-font { font-family: Georgia, Garamond, 'Times New Roman', serif; }
.navbar-light .navbar-brand { color: white; }
.navbar-light .navbar-brand:hover { color: yellow; }
.navbar-light .navbar-brand:focus { color: khaki; }
.navbar-light .navbar-brand { font-family: Georgia, Garamond, 'Times New Roman', serif; }
.nav-link { font-family: Georgia, Garamond, 'Times New Roman', serif; }@page
@model ObliqueTriangles2.Pages.AASModel
@{
string? strMessage = null;
float side1 = 0.00f, side2 = 0.00f, side3 = 0.00f;
float angle1 = 0.00F, angle2 = 0.00F, angle3 = 0.00F;
if (Request.HasFormContentType)
{
try
{
angle1 = float.Parse(Request.Form["txtAASAngle1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the lower left angle of the AAS shape.";
}
try
{
angle2 = float.Parse(Request.Form["txtAASAngle2"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the lower right angle of the AAS shape.";
}
try
{
side1 = float.Parse(Request.Form["txtAASSide1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the right side of the AAS shape.";
}
// Here, we use the law of sines
angle3 = 180 - (angle1 + angle2);
side2 = side1 * MathF.Sin(angle2 * MathF.PI / 180) / MathF.Sin(angle1 * MathF.PI / 180);
side3 = side1 * MathF.Sin(angle3 * MathF.PI / 180) / MathF.Sin(angle1 * MathF.PI / 180);
}
}
<div class="delimiter common-font">
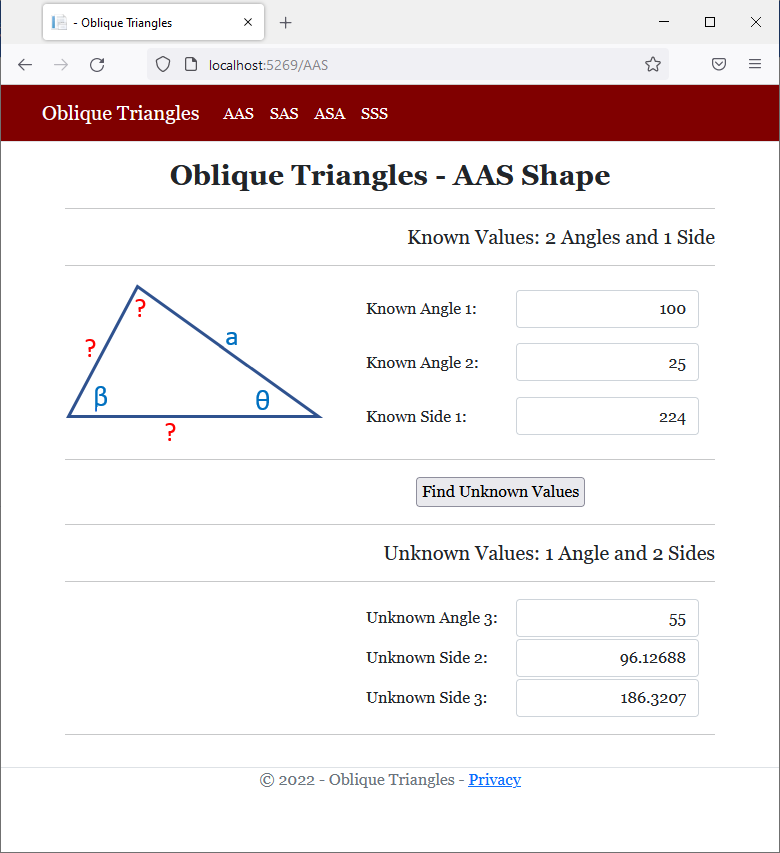
<h2 class="text-center bold">Oblique Triangles - AAS Shape</h2>
<hr />
<h5 class="text-right">Known Values: 2 Angles and 1 Side</h5>
<hr />
<form name="frmGeometry" method="post">
<table>
<tr>
<td style="width: 300px" rowspan="3">
<img src="~/images/aas.png" width="258" height="159" alt="Oblique Triangles - AAS Shape">
</td>
<td style="width: 150px">Known Angle 1:</td>
<td>@Html.TextBox("txtAASAngle1", @angle1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Angle 2:</td>
<td>@Html.TextBox("txtAASAngle2", @angle2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 1:</td>
<td>@Html.TextBox("txtAASSide1", @side1, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<table>
<tr>
<td style="width: 350px"> </td>
<td style="text-align: center"><input type="submit" name="btnSubmit" value="Find Unknown Values" /></td>
</tr>
</table>
</form>
<hr />
<h5 class="text-right">Unknown Values: 1 Angle and 2 Sides</h5>
<hr />
<table>
<tr>
<td style="width: 300px"> </td>
<td style="width: 150px">Unknown Angle 3:</td>
<td>@Html.TextBox("txtAASAngle3", @angle3, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Side 2:</td>
<td>@Html.TextBox("txtAASSide2", @side2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Side 3:</td>
<td>@Html.TextBox("txtAASSide3", @side3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<p class="text-center">@strMessage</p>
</div>@page
@model ObliqueTriangles2.Pages.SASModel
@{
string? strMessage = null;
float side1 = 0.00f, side2 = 0.00f, side3 = 0.00f;
float angle1 = 0.00F, angle2 = 0.00F, angle3 = 0.00F;
if (Request.HasFormContentType)
{
try
{
side1 = float.Parse(Request.Form["txtSASSide1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for one of the known sides of the SAS shape.";
}
try
{
angle1 = float.Parse(Request.Form["txtSASAngle1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the known angle of the SAS shape.";
}
try
{
side2 = float.Parse(Request.Form["txtSASSide2"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the other known side of the SAS shape.";
}
// Here, we use the law of cosines
side3 = MathF.Sqrt((side1 * side1) +
(side2 * side2) -
(2 * side1 * side2 * MathF.Cos(angle1 * MathF.PI / 180)));
angle2 = MathF.Acos(((side3 * side3) +
(side2 * side2) -
(side1 * side1)) /
(2 * side3 * side2)) * 180 / MathF.PI;
angle3 = 180 - (angle1 + angle2);
}
}
<div class="delimiter common-font">
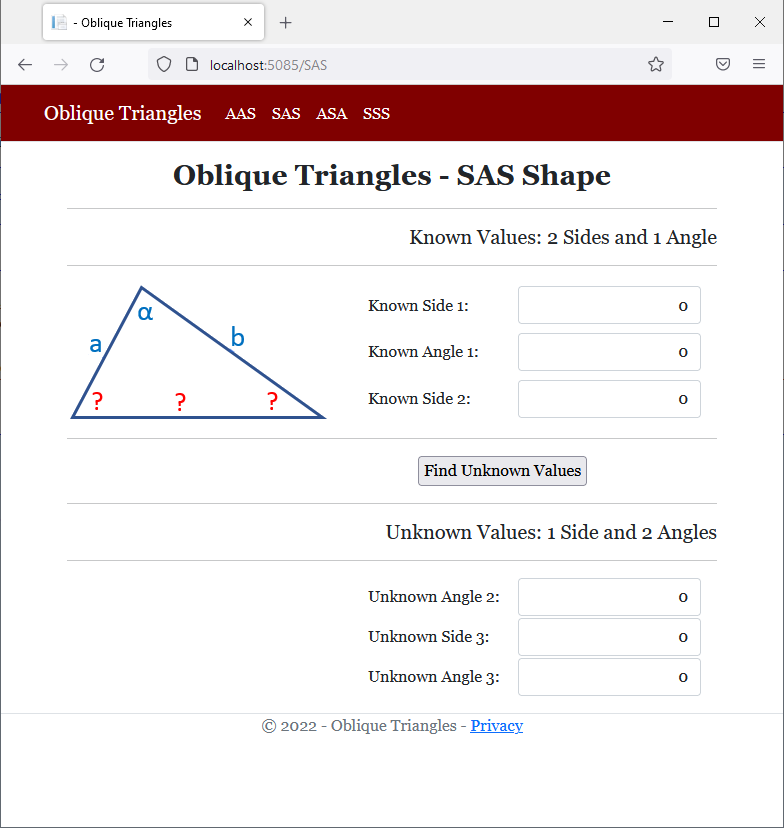
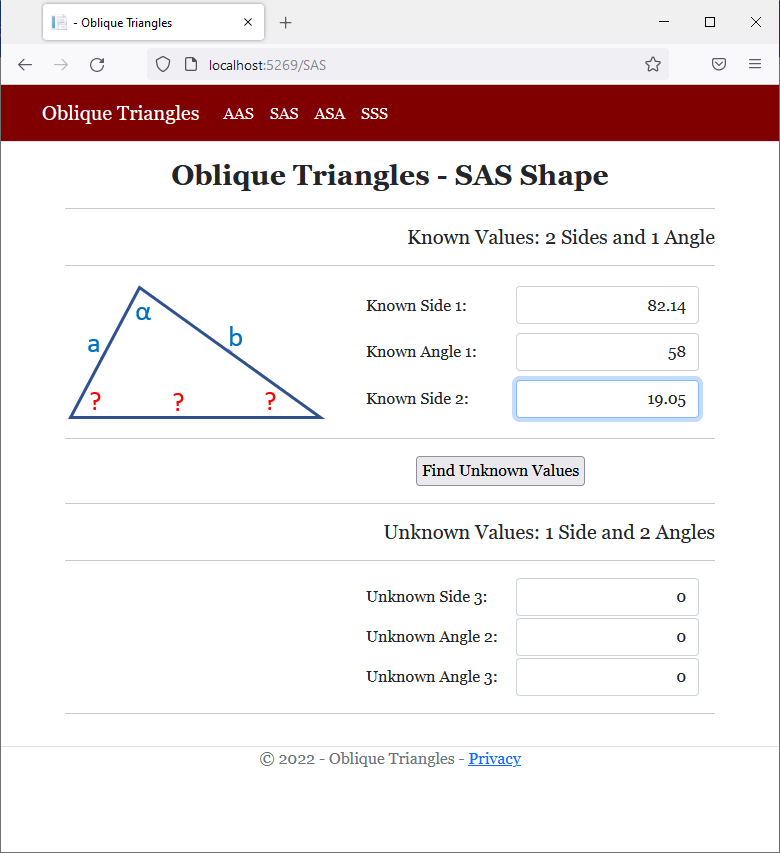
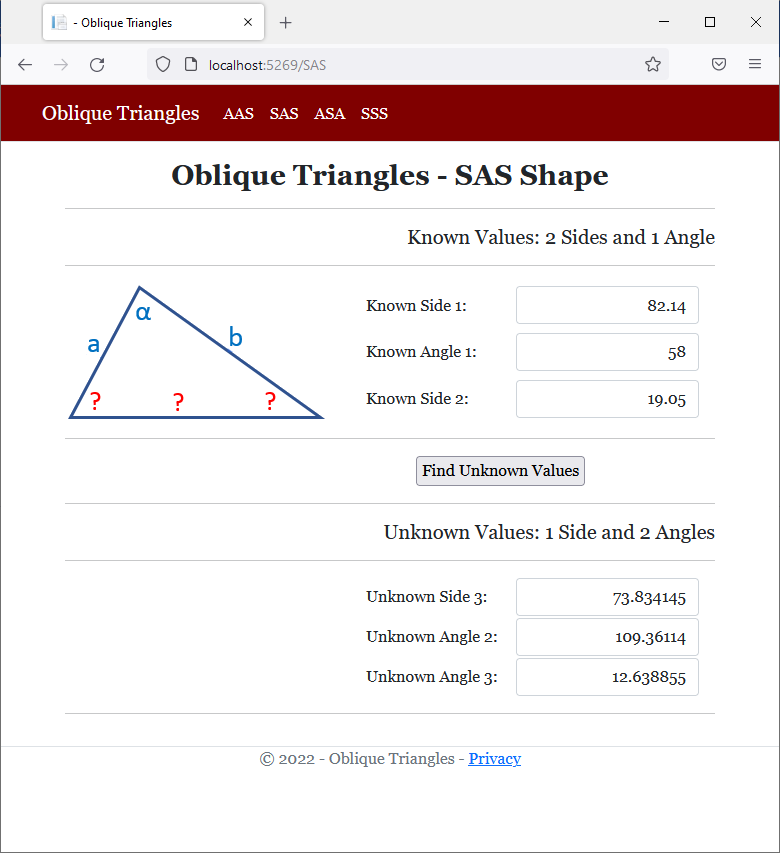
<h2 class="text-center bold">Oblique Triangles - SAS Shape</h2>
<hr />
<h5 class="text-right">Known Values: 2 Sides and 1 Angle</h5>
<hr />
<form name="frmGeometry" method="post">
<table>
<tr>
<td style="width: 300px" rowspan="3">
<img src="~/images/sas.png" width="260" height="138" alt="Oblique Triangles - SAS Shape">
</td>
<td style="width: 150px">Known Side 1:</td>
<td>@Html.TextBox("txtSASSide1", @side1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Angle 1:</td>
<td>@Html.TextBox("txtSASAngle1", @angle1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 2:</td>
<td>@Html.TextBox("txtSASSide2", @side2, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<table>
<tr>
<td style="width: 350px"> </td>
<td style="text-align: center"><input type="submit" name="btnSubmit" value="Find Unknown Values" /></td>
</tr>
</table>
</form>
<hr />
<h5 class="text-right">Unknown Values: 1 Side and 2 Angles</h5>
<hr />
<table>
<tr>
<td style="width: 300px"> </td>
<td style="width: 150px">Unknown Angle 2:</td>
<td>@Html.TextBox("txtSASAngle2", @angle2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Side 3:</td>
<td>@Html.TextBox("txtSASSide3", @side3, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Angle 3:</td>
<td>@Html.TextBox("txtSASAngle3", @angle3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<p class="text-center">@strMessage</p>
</div>@page
@model ObliqueTriangles2.Pages.ASAModel
@{
string? strMessage = null;
float side1 = 0.00f, side2 = 0.00f, side3 = 0.00f;
float angle1 = 0.00F, angle2 = 0.00F, angle3 = 0.00F;
if (Request.HasFormContentType)
{
try
{
angle1 = float.Parse(Request.Form["txtASAAngle1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for one of the known angles of the ASA shape.";
}
try
{
side1 = float.Parse(Request.Form["txtASASide1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the side that is between the angles whose values are about the ASA shape.";
}
try
{
angle2 = float.Parse(Request.Form["txtASAAngle2"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the other known angle of the ASA oblique triangle.";
}
// Here, we use the law of sines
angle3 = 180 - (angle1 + angle2);
side2 = side1 * MathF.Sin(angle2 * MathF.PI / 180) / MathF.Sin(angle1 * MathF.PI / 180);
side3 = side1 * MathF.Sin(angle3 * MathF.PI / 180) / MathF.Sin(angle1 * MathF.PI / 180);
}
}
<div class="delimiter common-font">
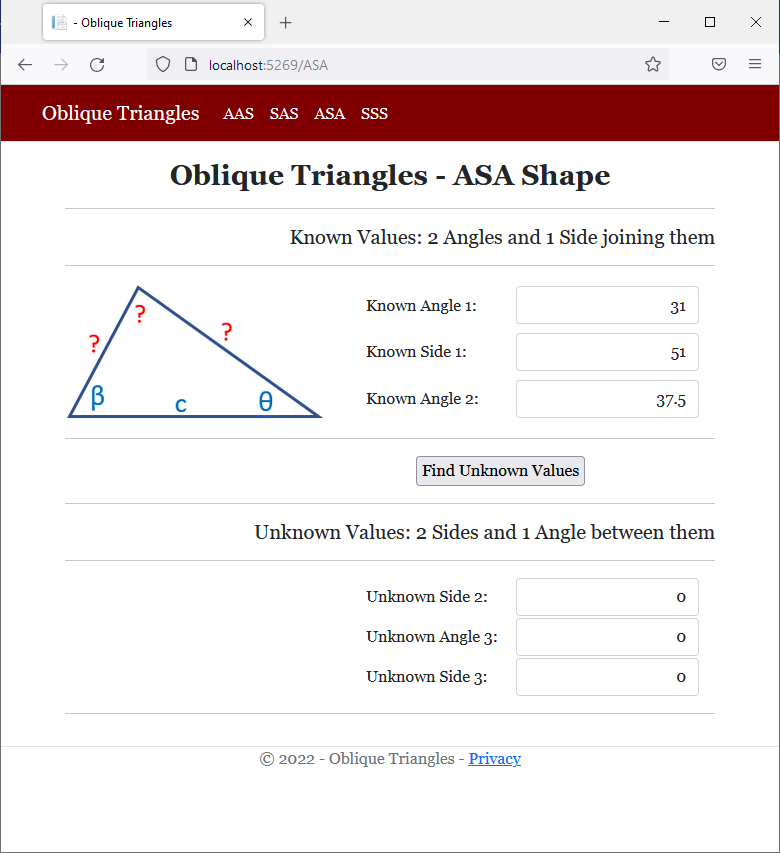
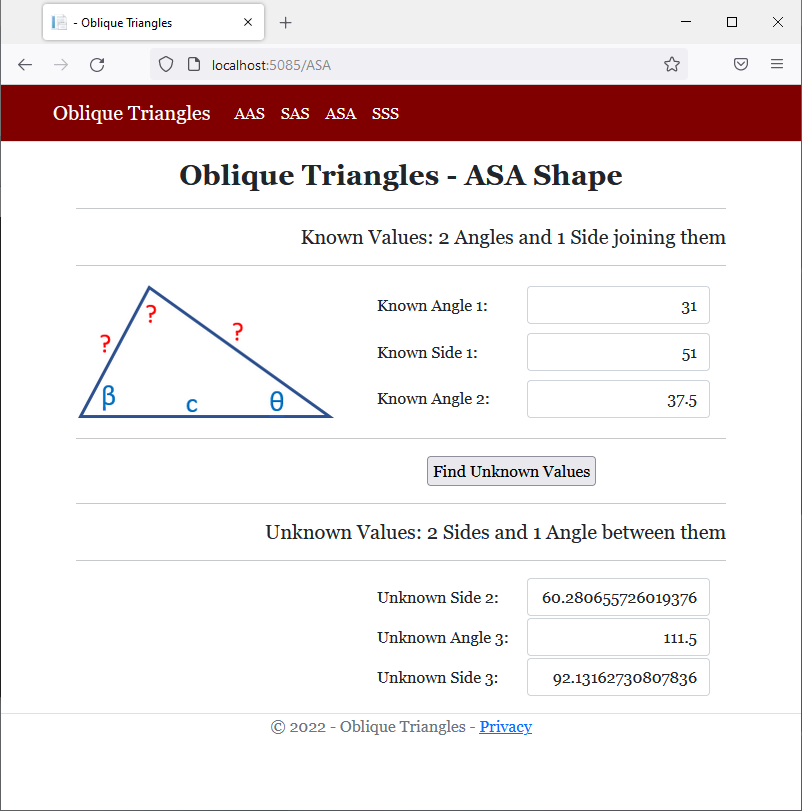
<h2 class="text-center bold">Oblique Triangles - ASA Shape</h2>
<hr />
<h5 class="text-right">Known Values: 2 Angles and 1 Side joining them</h5>
<hr />
<form name="frmGeometry" method="post">
<table>
<tr>
<td style="width: 300px" rowspan="3">
<img src="~/images/asa.png" width="260" height="138" alt="Oblique Triangles - SAS Shape">
</td>
<td style="width: 150px">Known Angle 1:</td>
<td>@Html.TextBox("txtASAAngle1", @angle1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 1:</td>
<td>@Html.TextBox("txtASASide1", @side1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Angle 2:</td>
<td>@Html.TextBox("txtASAAngle2", @angle2, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<table>
<tr>
<td style="width: 350px"> </td>
<td style="text-align: center"><input type="submit" name="btnSubmit" value="Find Unknown Values" /></td>
</tr>
</table>
</form>
<hr />
<h5 class="text-right">Unknown Values: 2 Sides and 1 Angle between them</h5>
<hr />
<table>
<tr>
<td style="width: 300px"> </td>
<td style="width: 150px">Unknown Side 2:</td>
<td>@Html.TextBox("txtASASide2", @side2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Angle 3:</td>
<td>@Html.TextBox("txtASAAngle3", @angle3, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Side 3:</td>
<td>@Html.TextBox("txtASASide3", @side3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<p class="text-center">@strMessage</p>
</div>@page
@model ObliqueTriangles2.Pages.SSSModel
@{
string? strMessage = null;
float side1 = 0.00f, side2 = 0.00f, side3 = 0.00f;
float angle1 = 0.00F, angle2 = 0.00F, angle3 = 0.00F;
if (Request.HasFormContentType)
{
try
{
side1 = float.Parse(Request.Form["txtSSSSide1"]);
}
catch (FormatException)
{
strMessage = "You must type a value for one of the known sides of the SSS shape.";
}
try
{
side2 = float.Parse(Request.Form["txtSSSSide2"]);
}
catch (FormatException)
{
strMessage = "You must type a value for another side of the SSS triangle.";
}
try
{
side3 = float.Parse(Request.Form["txtSSSSide3"]);
}
catch (FormatException)
{
strMessage = "You must type a value for the remaining known side of the SSS oblique triangle.";
}
// Here, we use the law of cosines
angle1 = MathF.Acos(((side3 * side3) +
(side2 * side2) -
(side1 * side1)) /
(2 * side3 * side2)) * 180 / MathF.PI;
angle2 = MathF.Acos(((side3 * side3) +
(side1 * side1) -
(side2 * side2)) /
(2 * side3 * side1)) * 180 / MathF.PI;
angle3 = 180 - (angle1 + angle2);
}
}
<div class="delimiter common-font">
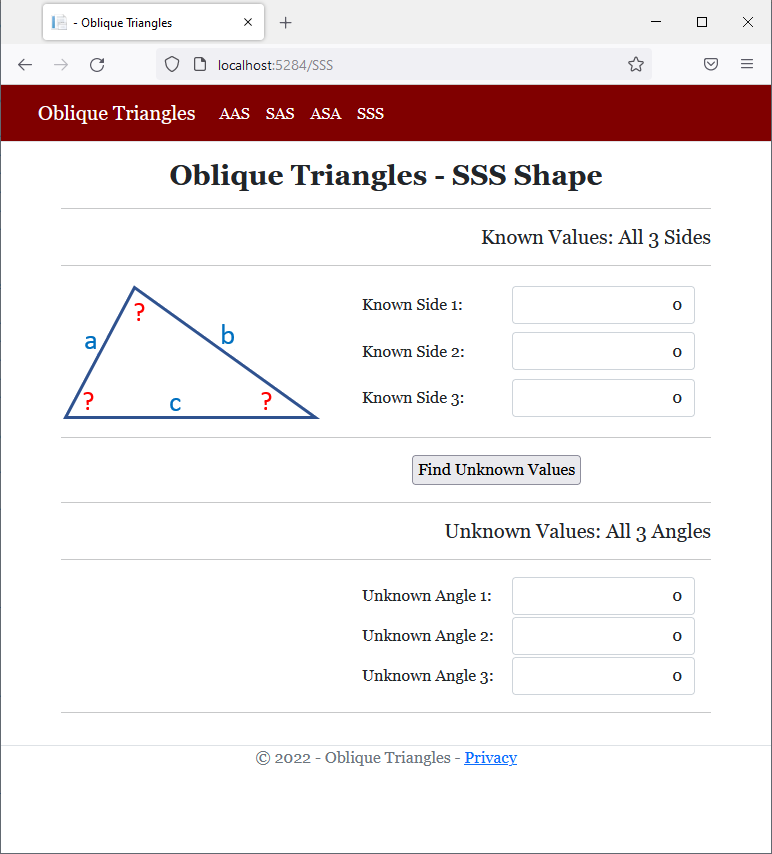
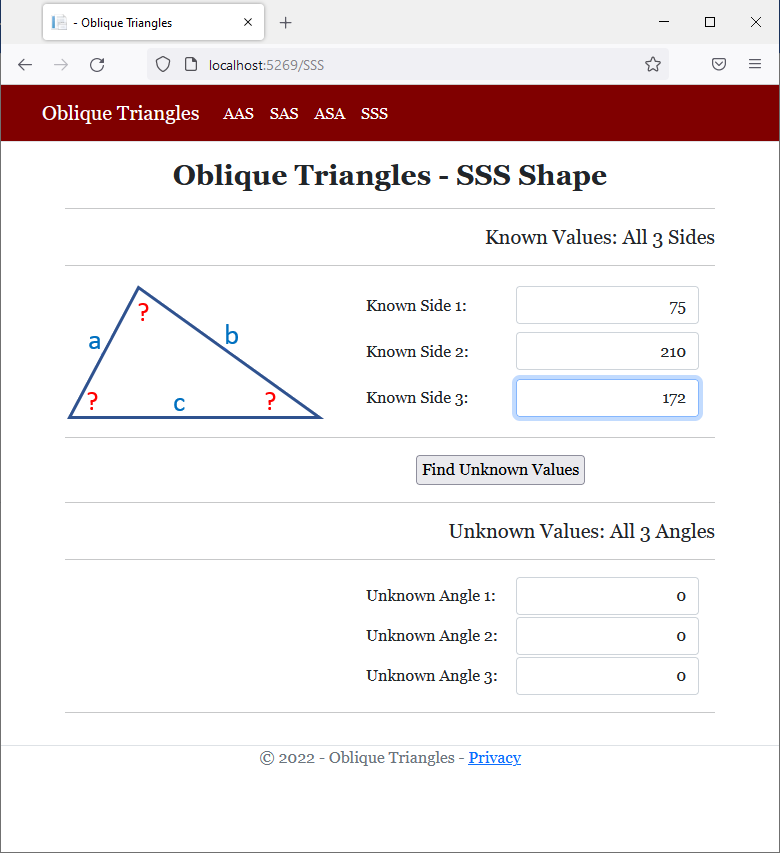
<h2 class="text-center bold">Oblique Triangles - SSS Shape</h2>
<hr />
<h5 class="text-right">Known Values: All 3 Sides</h5>
<hr />
<form name="frmGeometry" method="post">
<table>
<tr>
<td style="width: 300px" rowspan="3">
<img src="~/images/sss.png" width="259" height="137" alt="Oblique Triangles - SSS Shape">
</td>
<td style="width: 150px">Known Side 1:</td>
<td>@Html.TextBox("txtSSSSide1", @side1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 2:</td>
<td>@Html.TextBox("txtSSSSide2", @side2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td>Known Side 3:</td>
<td>@Html.TextBox("txtSSSSide3", @side3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<table>
<tr>
<td style="width: 350px"> </td>
<td style="text-align: center"><input type="submit" name="btnSubmit" value="Find Unknown Values" /></td>
</tr>
</table>
</form>
<hr />
<h5 class="text-right">Unknown Values: All 3 Angles</h5>
<hr />
<table>
<tr>
<td style="width: 300px"> </td>
<td style="width: 150px">Unknown Angle 1:</td>
<td>@Html.TextBox("txtSSSAngle1", @angle1, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Angle 2:</td>
<td>@Html.TextBox("txtSSSAngle2", @angle2, new { @class = "form-control text-right" })</td>
</tr>
<tr>
<td> </td>
<td>Unknown Angle 3:</td>
<td>@Html.TextBox("txtSSSAngle3", @angle3, new { @class = "form-control text-right" })</td>
</tr>
</table>
<hr />
<p class="text-center">@strMessage</p>
</div><!DOCTYPE html>
<html lang="en">
<head>
<meta charset="utf-8" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>@ViewData["Title"] - Oblique Triangles</title>
<link rel="stylesheet" href="~/lib/bootstrap/dist/css/bootstrap.min.css" />
<link rel="stylesheet" href="~/css/site.css" asp-append-version="true" />
<link rel="stylesheet" href="~/css/Geometry.css" asp-append-version="true" />
</head>
<body>
<header>
<nav class="navbar navbar-expand-sm navbar-toggleable-sm navbar-light bg-white border-bottom box-shadow mb-3 top-bar">
<div class="container">
<a class="navbar-brand" asp-area="" asp-page="/Index">Oblique Triangles</a>
<button class="navbar-toggler" type="button" data-bs-toggle="collapse" data-bs-target=".navbar-collapse" aria-controls="navbarSupportedContent"
aria-expanded="false" aria-label="Toggle navigation">
<span class="navbar-toggler-icon"></span>
</button>
<div class="navbar-collapse collapse d-sm-inline-flex justify-content-between">
<ul class="navbar-nav flex-grow-1">
<li class="nav-item">
<a class="nav-link text-white" asp-area="" asp-page="/AAS">AAS</a>
</li>
<li class="nav-item">
<a class="nav-link text-white" asp-area="" asp-page="/SAS">SAS</a>
</li>
<li class="nav-item">
<a class="nav-link text-white" asp-area="" asp-page="/ASA">ASA</a>
</li>
<li class="nav-item">
<a class="nav-link text-white" asp-area="" asp-page="/SSS">SSS</a>
</li>
</ul>
</div>
</div>
</nav>
</header>
<div class="container">
<main role="main" class="pb-3">
@RenderBody()
</main>
</div>
<footer class="border-top footer text-muted">
<div class="container">
<p class="text-center common-font">© 2022 - Oblique Triangles - <a asp-area="" asp-page="/Privacy">Privacy</a></p>
</div>
</footer>
<script src="~/lib/jquery/dist/jquery.min.js"></script>
<script src="~/lib/bootstrap/dist/js/bootstrap.bundle.min.js"></script>
<script src="~/js/site.js" asp-append-version="true"></script>
@await RenderSectionAsync("Scripts", required: false)
</body>
</html>


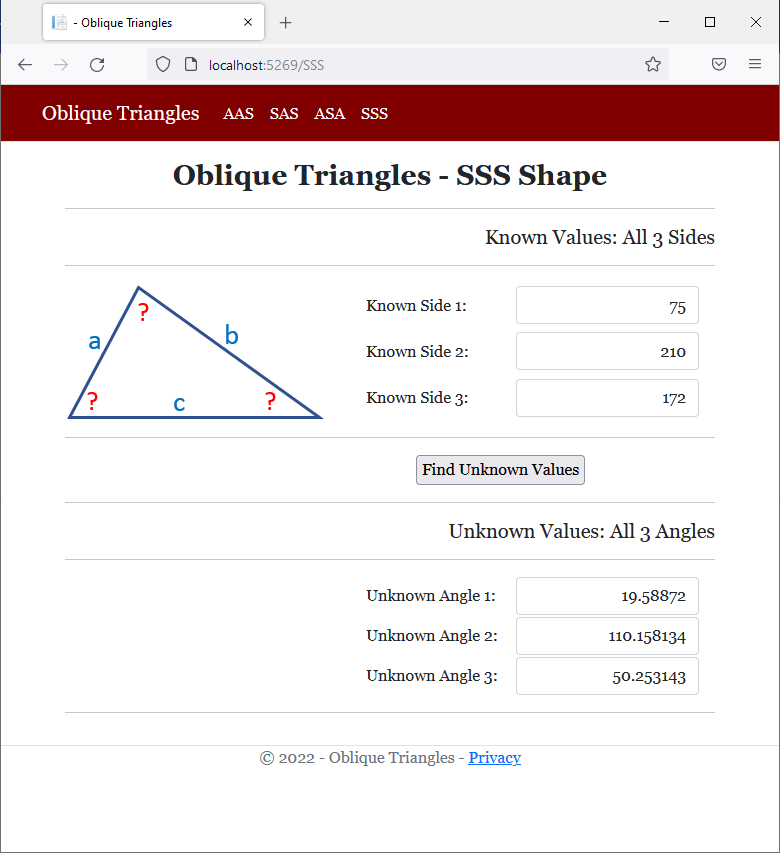
Characteristics of Floating-Point Numbers
The Minimum Value of a Type
Like integers, floating-point numbers have limits so they can fit in the computer memory allocated for them. As seen for the structures of integers, to let you get the lowest value that a type can hold, each number-associated structure is equipped with a constant field named MinValue. For the float and Single type, this field is defined as follows:
public const float MinValue = -3.40282347E+38;
To get the lowest value of a type, you can access this field. Here is an example:
@page
@model Exercises.Pages.ExerciseModel
@{
}
<pre>===========================================================================================
Float Minimum Value (Natural): @float.MinValue.ToString("N")
Float Minimum Value (Exponential): @float.MinValue.ToString("E")
===========================================================================================</pre>
This would produce:
=========================================================================================== Float Minimum Value (Natural): -340,282,346,638,528,859,811,704,183,484,516,925,440.00 Float Minimum Value (Exponential): -3.402823E+038 ===========================================================================================
The Maximum Value of a Type
To let you get the highest value that a floating-point number can hold, their structure is equipped with a constant field named MaxValue. For the float type, this field is defined as follows:
public const float MaxValue = 3.40282347E+38;
To get the highest value of a type, access this field. Here is an example:
@page
@model Exercises.Pages.ExerciseModel
@{
}
<pre>===========================================================================================
Float Minimum Value (Natural): @float.MinValue.ToString("N")
Float Minimum Value (Exponential): @float.MinValue.ToString("E")
Float Maximum Value (Natural): @float.MaxValue.ToString("N")
Float Maximum Value (Exponential): @float.MaxValue.ToString("E")
===========================================================================================</pre>
This would produce:
=========================================================================================== Float Minimum Value (Natural): -340,282,346,638,528,859,811,704,183,484,516,925,440.00 Float Minimum Value (Exponential): -3.402823E+038 Float Maximum Value (Natural): 340,282,346,638,528,859,811,704,183,484,516,925,440.00 Float Maximum Value (Exponential): 3.402823E+038 ===========================================================================================
When the Value is Not-A-Number
After declaring and initializing a float (or a Single) variable, it should hold an appropriate value. If you get the variable value some other way, at one time or another, you may not know what value is stored in the memory allocated for the variable. In fact, the variable may hold a value that is not a number. To let you check whether the variable is holding a value that is not a number, the Single structure of the floating-point type is equipped with a constant named NaN. To get its information, type the float data type, followed by the period operator, and followed by the NaN constant. Here is an example:
@{
floatnumber = 0D;
string msg = "";
if(number == double.NaN)
msg = "The value is not a number."
}
Another technique you can use to check this characteristic is to call the IsNaN() method is the Single structure.
The Epsilon Constant
Using one integer and one floating-point number, or with two floating-point numbers, you can perform one of the routine arithmetic operations such as the addition, the subtraction, the multiplication, or the division. When it comes to the division and if performed on two constants, you can get a positive or a negative number. In highly precise calculations, you may have to deal with an approximate number whose exact value is not known. For example, the smallest positive number is called epsilon. In the Single structure, this constant is named Epsilon. For the single-precision type, the epsilon is equal to 1.445.
The Negative Infinity
When dealing with real numbers, some operations produce very little or very large numbers. In algebra, the smallest conceptual number is called negative infinity (in reality, infinity is not a number but a concept). In the .NET library, the negative infinity is represented by a constant named NegativeInfinity. To access this number, type float, followed by a period operator, followed by the name of this constant.
To let you find out whether a variable holds a negative infinity value, the structures of the floating-point number is equipped with a method named IsNegativeInfinity. The syntax of this method is:
public static bool IsNegativeInfinity(float f);
The Positive Infinity
On the other extreme, the possible largest number is named positive infinity. This constant is represented in the .NET library by the PositiveInfinity value. To access this constant, type float, a period, and this constant. To find out if a variable's value is a positive infinity, you can call its IsPositiveInfinity() method. The syntax of this method ise:
public static bool IsPositiveInfinity(float f);
To check whether the value of a variable is one of the infinities, you can call its IsInfinity() method. The syntax of this method is:
public static bool IsInfinity(float f);
Double-Precision Numbers
Introduction
When a variable is larger than the float can handle and requires more precision, you should declare it using either the var or the double keyword. Here is an example:
@{
var number = 62834.9023;
}
<p>Number: " @number</p>
This would produce:
Number: 62834.9023
A variable declared as double uses 64 bits to store very large numbers ranging from 1.79769313486232e308 to 1.79769313486232e308 with a precision of 15 or 16 digits.
A Double-Precision Number
To support numbers with double-precision, the .NET library provides a structure named Double. This structure is equipped with the same members as the Single structure. These include the minimum and the maximum values. Here are examples:
@page
@model Exercises.Pages.ExerciseModel
@{
}
<pre>===========================================================================================
Float Minimum Value (Natural): " + float.MinValue.ToString("N")
Float Minimum Value (Exponential): " + float.MinValue.ToString("E")
Float Maximum Value (Natural): " + float.MaxValue.ToString("N")
Float Maximum Value (Exponential): " + float.MaxValue.ToString("E")
-------------------------------------------------------------------------------------------
Double Minimum Value (Natural): " + double.MinValue.ToString("N")
Double Minimum Value (Exponential): " + double.MinValue.ToString("E")
Double Maximum Value (Natural): " + double.MaxValue.ToString("N")
Double Maximum Value (Exponential): " + double.MaxValue.ToString("E")
===========================================================================================</pre>
This would produce:
=========================================================================================== Float Minimum Value (Natural): -340,282,346,638,528,859,811,704,183,484,516,925,440.00 Float Minimum Value (Exponential): -3.402823E+038 Float Maximum Value (Natural): 340,282,346,638,528,859,811,704,183,484,516,925,440.00 Float Maximum Value (Exponential): 3.402823E+038 ------------------------------------------------------------------------------------------- Double Minimum Value (Natural): -179,769,313,486,231,570,814,527,423,731,704,356,798,070,567,525,844,996,598,917,476,803,157,260,780,028,538,760,589,558,632,766,878,171,540,458,953,514,382,464,234,321,326,889,464,182,768,467,546,703,537,516,986,049,910,576,551,282,076,245,490,090,389,328,944,075,868,508,455,133,942,304,583,236,903,222,948,165,808,559,332,123,348,274,797,826,204,144,723,168,738,177,180,919,299,881,250,404,026,184,124,858,368.00 Double Minimum Value (Exponential): -1.797693E+308 Double Maximum Value (Natural): 179,769,313,486,231,570,814,527,423,731,704,356,798,070,567,525,844,996,598,917,476,803,157,260,780,028,538,760,589,558,632,766,878,171,540,458,953,514,382,464,234,321,326,889,464,182,768,467,546,703,537,516,986,049,910,576,551,282,076,245,490,090,389,328,944,075,868,508,455,133,942,304,583,236,903,222,948,165,808,559,332,123,348,274,797,826,204,144,723,168,738,177,180,919,299,881,250,404,026,184,124,858,368.00 Double Maximum Value (Exponential): 1.797693E+308 ===========================================================================================
Characteristics of a Double-Precision Value
The Epsilon Constant
The double data type uses the same characteristics we reviewed for the float data type and its accompanying Single structure. The members of their structures are the same, Only some values are different. As we saw, the smallest positive number is the epsilon. For a double-precision type, the epsilon constant is equivalent to 4.94065645841247-324.
A Better Floating-Point Number
Because the double data type provides a better result with better precision than the float, whenever you declare a variable using either the var or the float keyword and assign it a value, the compiler allocates 64 bits to store the values of the variable. If you insist on the variable being treated as float, when assigning it a value, add an f or an F suffix to the value. Here is an example:
@page
@model Exercises.Pages.ExerciseModel
@{
float distance = 248.38F;
}
<pre>Distance: @distance km
========================</pre>
This would produce:
Distance: 248.38 km ========================
This would produce:
Distance = 248.38km
Remember that if you declare the variable as var and want to treat it as a value with single precision, add an f or an F suffix to the value assigned to it. Here is an example:
@page
@model Exercises.Pages.ExerciseModel
@{
var number = 62834.9023F;
}
<pre>Number: @number
========================</pre>
This would produce:
Number: 62834.902 ========================
On the other hand, if you want a value to be treated with double-precision, add a d or a D suffix to it. Here is an example:
@{
var number = 62834.9023D;
}
<pre>Number: @number
========================
This would produce:
Number: 62834.9023 ========================</pre>
Introduction
To support small to extremely large numbers, the C# language provides a data type named decimal. Use that keyword to declare a variable that would hold significantly large values that can be stored in a combination of 128 bits. The values stored in a decimal variable can range from -79,228,162,514,264,337,593,543,950,335 to 79,228,162,514,264,337,593,543,950,335.
Initializing a Decimal
After declaring a decimal variable, you can initialize it with a natural number. To indicate that the variable holds a decimal value, when initializing it, add an m or an M suffix to its value.
To let you display a decimal number to the console screen, both the Console.Write() and the Console.WriteLine() methods each has a syntax that takes a decimal argument. Their syntaxes are:
public static void Write(decimal value); public static void WriteLine(decimal value);
Here is an example:
@page
@model Exercises.Pages.ExerciseModel
@{
decimal hourlySalary = 24.25M;
}
<pre>Hourly Salary = @hourlySalary
========================</pre>
This would produce:
Hourly Salary = 24.25 ========================
Decimal Number Support
To support numeric values with high precision, the .NET library provides a structure named Decimal. This structure provides the characteristics of the C#'s decimal type. The structure has the same members we reviewed for the Single and the Double structures.
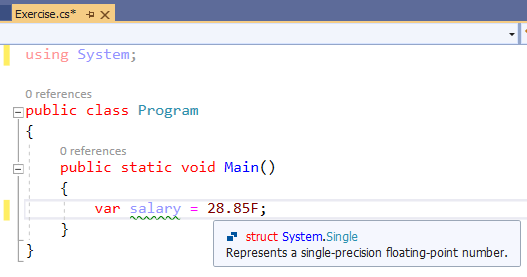
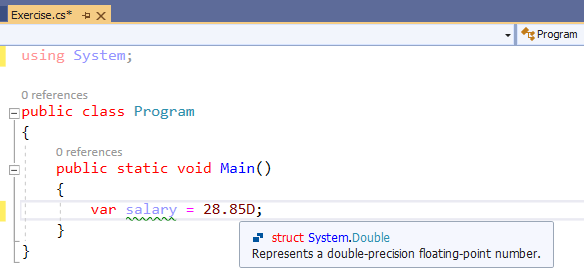
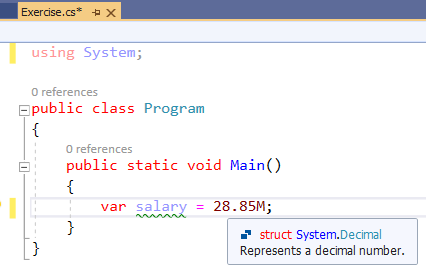
Distinguishing the Floating-Point Variables
As seen in previous sections and this one, when declaring and initializing a real variable, the suffix you give to its assigned value indicates to the compiler the actual type of value and the type of memory that would be allocated for the variable:
The Boolean Type
Introduction
As seen in previous lessons, the bool data type is used to represent a value considered as being true or false. In the .NET library, the bool data type is represented by a structure named Boolean. The true value of a bool variable is represented by a field named TrueString. The false value is represented by a field named FalseString. In other words, when true (or false) is represented as a string, "true" (or "false") is the same as TrueString (or FalseString).
Parsing a Boolean Variable
You can retrieve the value of a Boolean variable from a user. To support this, the Boolean structure is equipped with a static method named Parse. The Boolean.Parse() method is declared as follows:
public static bool Parse(string value);
This method takes as argument a string. The argument must contain either the word True or the word False (case-insensitive in both cases). If the argument is passed as "True", the method returns true. If the argument is "false", this method returns false.
When calling the Boolean.Parse() method to retrieve the value of a Boolean variable, if the supplied value is "True" or "False", the compiler would process it. If the value is not valid, the program would produce an error.
To avoid the error, the Boolean structure provides the TryParse() method. Its syntax is:
public static bool TryParse(string value, out bool result);
The first argument is the value to be parsed. If that value is valid, the second argument holds the True or False value of the first.
Consider the following code:
bool alt; bool HouseHas3Bedrooms = bool.TryParse("False", out alt);
The first argument returns True although it was passed as False. This means that, if the value of the first argument is valid, it is the second argument, not the first, that holds the result. If the first argument is not valid, the second argument returns a False value. Consider the following version of the program:
bool alt; bool HouseHas3Bedrooms = bool.TryParse("Don't Know", out alt);
|
|
|||
| Previous | Copyright © 2001-2022, FunctionX | Wednesday 09 February 2022 | Next |
|
|
|||